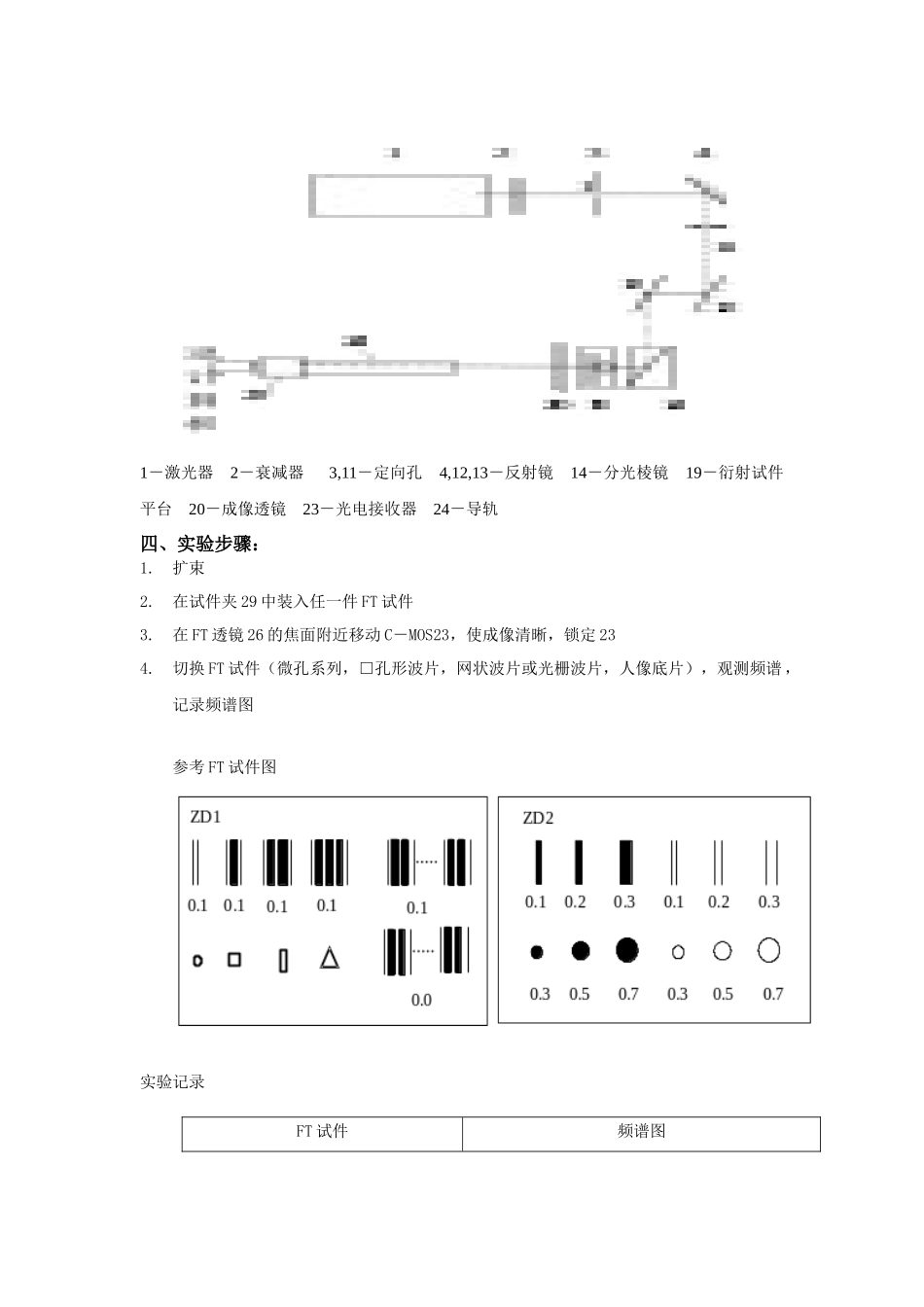
实验三 透镜的 FT 性质及常用函数与图形的光学频谱分析一、实验目的: 1.了解透镜对入射波前的相位调制原理2.加深对透镜复振幅传递函数透过率物理意义的认识(参见实验十一实验原理)3.应用光学频谱分析系统观察常见图形的傅里叶(FT)频谱,加深空间频率域的概念二、实验原理:理论基础:波动方程、复振幅、光学传递函数透镜由于本身厚度变化,使得入射光在通过透镜时,各处走过的光程不同,即所受时间延迟不同,因而具有位相调制能力,下图为简化分析,假设任意点入射的光线在透镜中的传播距离等于该点沿光轴方向透镜的厚度,并忽略光强损失,即通过透镜的光波振幅分布不变,仅产生大小正比于透镜各点厚度的位相变化,透镜传递函数记为:t(x,y)=exp[jΦ(x,y)] (1) Φ(x,y)=kL(x,y)L(x,y):表示光程 MNL(x,y)=nD(x,y)+[D0-D(x,y)] (2) D0:透镜中心厚度。D:透镜厚度。n:透镜折射率。可见只要知道透镜厚度函数 D(x,y)可得出其位相调制,在球面透镜傍轴区域,用抛物面近似球面,可得到球面透镜的厚度函数:D (x, y )=D 0−12(x2+ y2)(1R1− 1R2) (3) R1,R2:构成透镜的两个球面的曲率半径。t (x , y )=exp ( jknD0)⋅exp[− jk (n−1) 12(x2+ y2)(1R1− 1R2)] (4)引入焦距 f,其定义式为1f =(n−1)(1R1− 1R2)代入(4)得:t (x , y )=exp( jknD0) exp[−jk2f(x2+ y2)]此即透镜位相调制的表达式。第一项位相因子仅表示透镜对于入射光波的常量位相延迟,不影响位相的空间分布,即波面形状。第二项起调制作用的因子,它表明光波通过透镜时的位相延迟与该点到透镜中心的距离平方成正比。而且与透镜的焦距有关。其物理意义在于,当入射光波ui (x , y )=1时,略去透镜的常量值相位延迟后,紧靠透镜之后的平面上复振幅分布为u' (x, y )=u(x , y )∗t (x , y )=exp[−j k2f(x2+ y2)]傍轴近似下,这是一个球面波,对于正透镜 f>0,这是一个向透镜后方距离 f 处的 F 会聚的球面波。对于负透镜 f〈0,这是一个由透镜前方距离|f|处的虚焦点 F 发散的球面波。可见波面的变化。正是透镜具有exp[− j k2f(x2+ y2)]的位相因子。当然,在非傍轴近似条件下,会有波像差。考虑透镜孔径后,t (x , y )=exp[− j k2f(x2+ y2)]⋅p (x, y )p(x,y)为透镜的光瞳函数p (x, y )=¿¿三、实验光路1-激光器 2-衰减器 3,11-定向孔 4,12,13-反射镜 14-分光棱镜 19-衍射试件...