中考复习课《最短路径问题》VIP专享VIP免费

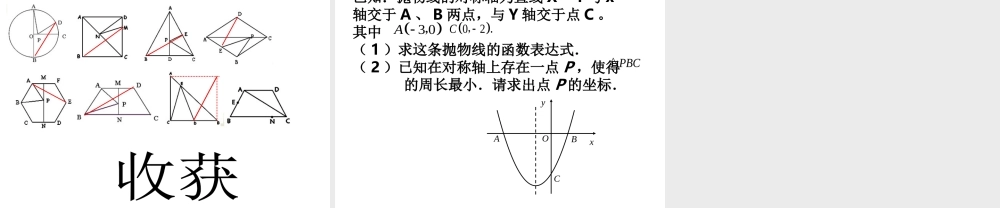
有关“最短”知多少两点之间线段最短点到直线的垂线段最短有关距离和最短： 1 两点一对称型 2 一点两对称型 3 两点两对称型 在正方形中探求线段和的最小值：如图所示，正方形 ABCD 的面积为 36 ，△ABE 是等边三角形，点 E 在正方形 ABCD内，在对角线 AC 上有一点 P ，使 PD ＋ PE 的和最小，则这个最小值为 变式 1 ：如图，正方形 ABCD 的边长为 8， M 在 DC 上，且 DM ＝ 2 ， N 是 AC上的一动点， DN ＋ MN 的最小值为 ( ) 变式 2 ：如图，在△ ABC 中， AC ＝ BC ＝ 2 ，∠ACB ＝ 90° ， D 是 BC 边的中点， E 是 AB 边上一动点，则 EC ＋ ED 的最小值为 _______ 在梯形中探求线段和的最小值如图，等腰梯形 ABCD 中，AB=AD=CD=1 ，∠ ABC=60 ° ，P 是对称轴直线 EF 上一点，则 PA+PB 的最小值为 ．CBAPD 变式：如图，在直角梯形 ABCD 中，∠ ABC＝ 90° ， AD∥BC ， AD ＝ 4 ， AB ＝ 5 ，BC ＝ 6 ，点 P 是 AB 上一个动点，当 PC ＋PD 的和最小时， PB 的长为 __ ． 在圆中探求线段和的最小值如图， AB 是⊙ O 的直径， AB=2 ， OC 是⊙O 的半径， OC⊥AB ，点 D 在 AC 上 ,AD=2CD ，点 P 是半径 OC 上一个动点，那么 AP+PD 的最小值是 .PADCOB⌒⌒ 变式：已知⊙ O 的直径 CD 为 4 ，∠ AOD 的度数为 60° ，点 B 是 AD 的中点，在直径 CD上找一点 P ，使 BP+AP 的值最小，并求 BP+AP 的最小值．⌒·OACD· B· 在平面直角坐标系下探求线段和的最小值 例 4 ： 在平面直角坐标系中，有 A （ 3 ，－ 2）， B （ 4 ， 2 ）两点，现另取一点 C （ 1 ， n），当 n =______ 时 ,AC + BC 的值最小． 变式 1 ：一次函数 y=-2x+4 的图象与 x 、 y 轴分别交于点A （ 2 ， 0 ）， B （ 0 ， 4), O 为坐标原点，设 OA 、 AB的中点分别为 C 、 D ， P 为 OB 上一动点，求 PC ＋ PD的最小值，并求取得最小值时 P 点坐标． 在矩形中探求线段和的最小值如图，在矩形 ABCD 中， AB ＝ 10 ， BC ＝5 ，若点 M ， N 分别是线段 AC ， AB 上的两个动点，则 BM+MN 最小值是（ ）CBAMDN 变式：在平面直角坐标系中 , 矩形 O ABC 如图 ,A 在 x 轴正半轴上 ,C 在 y 轴正半轴上OA=6,OC=4,D 为 OCOA=6,OC=4 ， D 为 OC中点， E 在 F 左侧， EF=2 ，当四边形 BDEF周长最小时， E 坐标为（ ）COBAEDF[ 课堂小结 ]“”构建 对称模型 实现转化已知：抛物线的对称轴为直线 X=-1 与 x轴交于 A 、 B 两点，与 Y 轴交于点 C 。其中（ 1 ）求这条抛物线的函数表达式．（ 2 ）已知在对称轴上存在一点 P ，使得 的周长最小．请求出点 P 的坐标．3 0A  ，02C，．PBC△ACxyBO