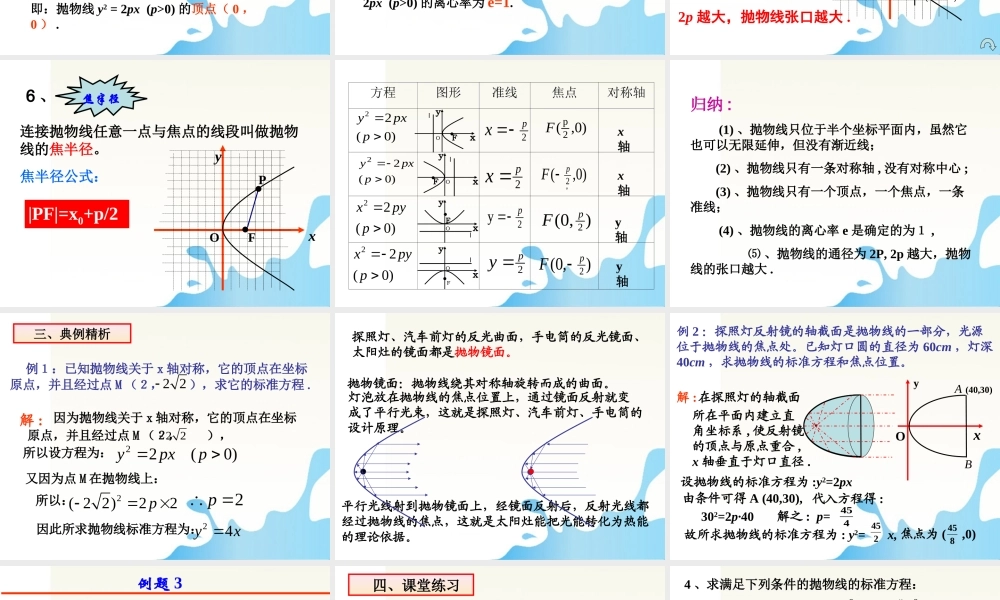
2.4.2 抛物线的简单几何性质 (1) 一、温故知新( 一 ) 圆锥曲线的统一定义 平面内,到定点 F 的距离与到定直线 l的距离比为常数 e 的点的轨迹 ,当 e > 1 时,是双曲线 .当 00) (2) 开口向左 y2 = -2px (p>0)(3) 开口向上 x2 = 2py (p>0) (4) 开口向下 x2 = -2py (p>0) 范围1 、yox)0,2( pF由抛物线 y2 =2px ( p>0 )220pxy有 0p 0x 所以抛物线的范围为0x 二、探索新知如何研究抛物线 y2 =2px ( p>0 )的几何性质 ? 对称性2 、yox)0,2( pF( , )x y关于 x 轴对称( ,)xy即点 (x,-y) 也在抛物线上 ,故 抛物线 y2 = 2px(p>0) 关于 x 轴对称 .则 (-y)2 = 2px若点 (x,y) 在抛物线上 , 即满足 y2 = 2px , 顶点3 、yox)0,2( pF 定义:抛物线与它的轴的交点叫做抛物线的顶点。y2 = 2px (p>0) 中,令 y=0, 则 x=0.即:抛物线 y2 = 2px (p>0) 的顶点( 0 ,0 ) . 离心率4 、yox)0,2( pFP(x,y) 抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。 由定义知, 抛物线 y2 = 2px (p>0) 的离心率为 e=1. xyOFABy2=2px2p过焦点而垂直于对称轴的弦AB ,称为抛物线的通径,利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图 .pp ,2 pp ,2|AB|=2p通径5 、2p 越大,抛物线张口越大 . 连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。|PF|=x0+p/2焦半径公式:焦半径6 、xyOFP 方程图形准线焦点对称轴)0(22ppxy)0(22ppxy)0(22ppyx)0(22ppyx)0,( 2pF)0,(2pF ),0(2pF),0(2pF2px2px 2yp2py x轴x轴y轴y轴oxFOylxFOylxFOylxFOyl 归纳 : (1) 、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线; (2) 、抛物线只有一条对称轴 , 没有对称中心 ; (3) 、抛物线只有一个顶点,一个焦点,一条准线; (4) 、抛物线的离心率 e 是确定的为1 , ⑸ 、抛物线的通径为 2P, 2p 越大,抛物线的张口越大 . 因为抛物线关于 x 轴对称,它的顶点在坐标原点,并且经过点 M (2, ),2 2解 :所以设方程为:)0(22ppxy又因为点...