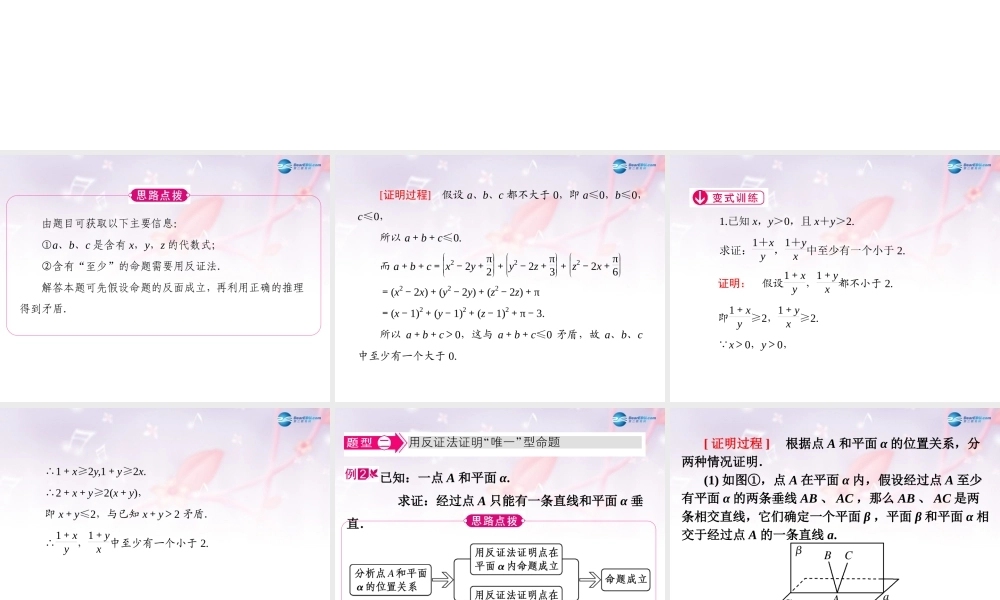
若 a、b、c 均为实数,且 a=x2-2y+π2,b=y2-2z+π3, c=z2-2x+π6.求证:a,b,c 中至少有一个大于 0. 由题目可获取以下主要信息: ①a、b、c 是含有 x,y,z 的代数式; ②含有“至少”的命题需要用反证法. 解答本题可先假设命题的反面成立,再利用正确的推理得到矛盾. [证明过程] 假设 a、b、c 都不大于 0,即 a≤0,b≤0,c≤0, 所以 a+b+c≤0. 而 a+b+c=x2-2y+π2 +y2-2z+π3 +z2-2x+π6 =(x2-2x)+(y2-2y)+(z2-2z)+π =(x-1)2+(y-1)2+(z-1)2+π-3. 所以 a+b+c>0,这与 a+b+c≤0 矛盾,故 a、b、c中至少有一个大于 0. 1.已知 x,y>0,且 x+y>2. 求证:1+xy ,1+yx 中至少有一个小于 2. 证明: 假设1+xy ,1+yx 都不小于 2. 即1+xy ≥2,1+yx ≥2. x>0,y>0, ∴1+x≥2y,1+y≥2x. ∴2+x+y≥2(x+y), 即 x+y≤2,与已知 x+y>2 矛盾. ∴1+xy ,1+yx 中至少有一个小于 2. 已知:一点 A 和平面 α. 求证:经过点 A 只能有一条直线和平面 α 垂直.[ 证明过程 ] 根据点 A 和平面 α 的位置关系,分两种情况证明.(1) 如图①,点 A 在平面 α 内,假设经过点 A 至少有平面 α 的两条垂线 AB 、 AC ,那么 AB 、 AC 是两条相交直线,它们确定一个平面 β ,平面 β 和平面 α 相交于经过点 A 的一条直线 a. 图①因为 AB⊥ 平面 α , AC⊥ 平面 α , a⊂α ,所以AB⊥a , AC⊥a ,在平面 β 内经过点 A 有两条直线都和直线 a 垂直,这与平面几何中经过直线上一点只能有已知直线的一条垂线相矛盾.(2) 如图②,点 A 在平面 α 外,假设经过点 A 至少有平面 α 的两条垂线 AB 和 AC(B 、 C 为垂足 ) ,那么 AB 、 AC 是两条相交直线,它们确定一个平面β ,平面 β 和平面 α 相交于直线 BC ,因为 AB⊥ 平面 α , AC⊥ 平面 α , BC⊂α ,所以 AB⊥BC , AC⊥BC. 图②在平面 β 内经过点 A 有两条直线都和 BC 垂直,这与平面几何中经过直线外一点只能有已知直线的一条垂线相矛盾.综上,经过一点 A 只能有平面 α 的一条垂线.2. 求证:过直线外一点有且只有一条直线和这条直线平行.证明: 点 P 在直线外,∴ 点 P 和直线 a...