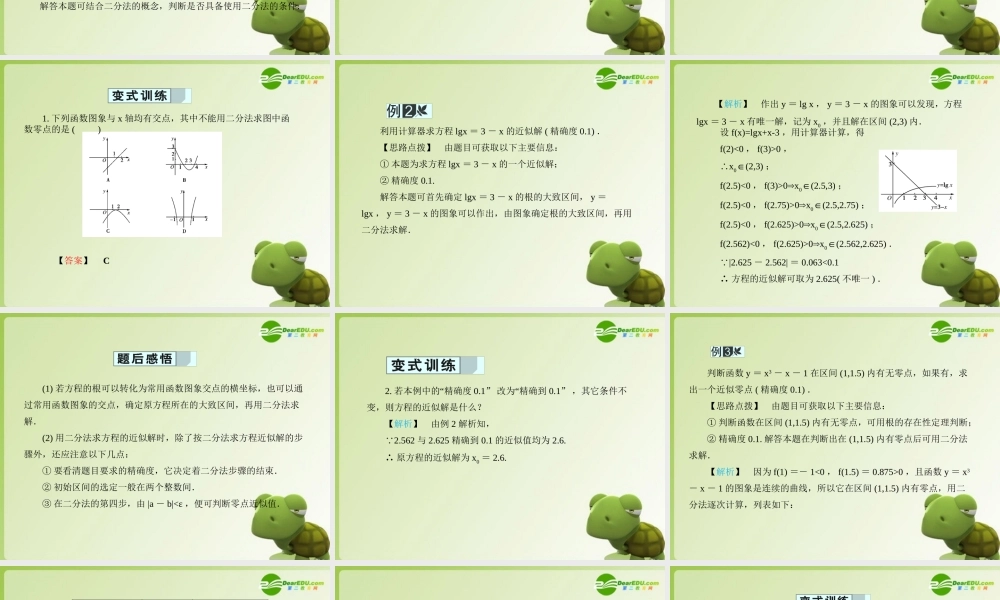
3.1.2 用二分法求方程的近似解1 .函数零点的判定如果函数 y = f(x) 在区间 [a , b] 上的图象是 _________ 的一条曲线,并且有 ,那么,函数 y = f(x) 在区间 (a , b) 内存在零点,即存在 c(a∈, b) ,使得 ,这个 c 也就是方程 f(x)= 0 的根.连续不变f(a)·f(b)<0f(c) = 01 .二分法的定义对于在区间 [a , b] 上 的函数 y = f(x) ,通过不断地把函数 f(x) 的零点所在的区间 ,使区间的两个端点 进而得到零点近似值的方法叫做二分法.2 .二分法的步骤给定精确度 ε ,用二分法求 f(x) 零点近似值的步骤如下:(1) 确定区间 [a , b] ,验证 ,给定精确度 ε ;(2) 求区间 (a , b) 的中点 c ;连续不断且 f(a)·f(b)<0一分为二逐步逼近零点f(a)f(b)<0(3) 计算 f(c) ;① 若 f(c) = 0 ,则 ;② 若 f(a)·f(c)<0 ,则令 b = c( 此时零点 x0∈ ;③ 若 f(c)·f(b)<0 ,则令 a = c( 此时零点 x0∈ .(4) 判断 a , b 是否达到精确度 ε :即若 |a - b|<ε ,则得到零点近似值 a( 或 b) ;否则重复 (2) ~ (4) .c 是零点(a , c)(c , b)1 .能否用二分法求任何函数 ( 图象是连续的 ) 的近似零点?【提示】 不能.看一个函数能否用二分法求其零点关键要看是否具备应用二分法的条件,即函数图象在零点附近是连续不断的,且在该零点左右函数值异号.2 .“精确度”与“精确到”是一回事吗?【提示】 不是.在某一“精确度”下的近似值不唯一,可以用区间内的任何一个数来表示;但是,“精确到”小数点后某一位的近似值是唯一的.下列函数图象与 x 轴均有交点,其中不能用二分法求图中函数零点的是 ( ) 【思路点拨】由题目可获取以下主要信息:① 题中给出了函数的图象;② 二分法的概念.解答本题可结合二分法的概念,判断是否具备使用二分法的条件.【解析 】利用二分法求函数零点必须满足零点两侧函数值异号.在 B 中,不满足 f(a)·f(b)<0 ,不能用二分法求零点,由于A 、 C 、 D 中零点两侧函数值异号,故可采用二分法求零点.故选B.【答案】 B(1) 准确理解“二分法”的含义.二分就是平均分成两部分.二分法就是通过不断地将所选区间一分为二,逐步逼近零点的方法,找到零点附近足够小的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点.(2)“ 二分法”与...