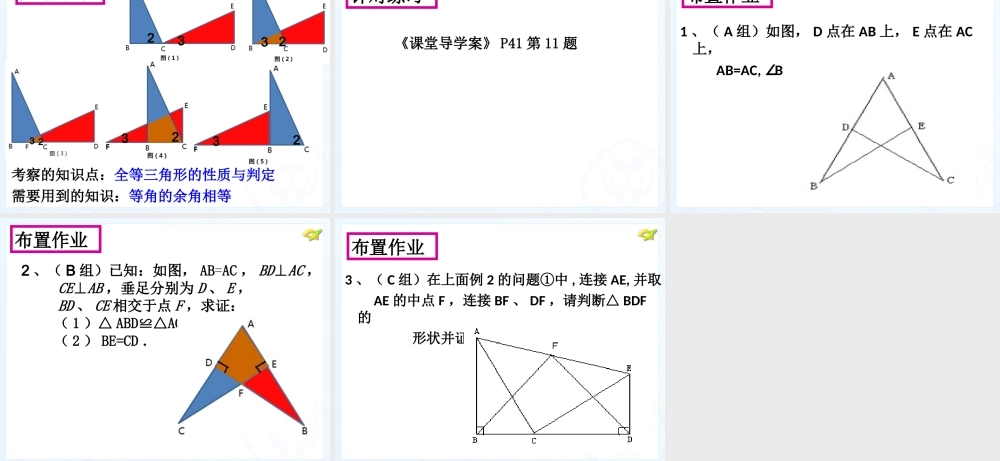
八年级 上册第十二章 全等三角形 小结与复习广州市海珠区黄埔初级中学 蔡映霞 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带哪一块去配?动动脑筋练习 1 、如图△ ABD ≌△EBC , AB=3cm , BC=5cm ,则 DE =__________做一做EDCBA2cm练习 2 、下列条件中,不能判定两个直角三角形 全等的是( )( A )一锐角和斜边对应相等 ( B )两条直角边对应相等( C )斜边和一直角边对应相等 ( D )两个锐角对应相等 做一做( AAS )( SAS )( HL )D练习 3 、已知 AB//DE ,且 AB=DE , 请你只添加一个条件,使△ ABC≌△DEF , 你添加的条件是 _______________ 理由是 ___________做一做DEFA BC 将一张矩形纸片沿着对角线剪开,得到两张全等三角形纸片,再将这两张三角形纸片放在桌面上,从平移、旋转、对称几个方面进行摆放,看看两个全等的三角形有一些怎样的特殊位置关系?拼一拼常见基本图形 1翻折、平移公共边平行线常见基本图形 2旋转公共边公共角123123常见基本图形 3平移132典型例题 如图⑴, AB⊥BD , DE⊥BD ,点 C 是 BD 上一点,且 BC=DE , AB=CD. ① 试判断 AC 与 CE 的关系,并说明理由 . ② 如图⑵,若把△ CDE 沿直线 BD 向左平移, 使△ CDE 的顶点 C 与 B 重合,此时 AC 与 BE 的关系还成立吗 ? 请说明理由。123123变式训练变式一: 如图 (3) , 若把图 (2) 中的△ BDE沿 直线 BD 向右平移, 使△ BDE 的顶 点 B 落在 F 的位置上,此时AC 与 EF 的关系还成立吗 ? 请说明理由。变式二: 如图 (4) , 若把图 (3) 中的 △ DEF沿 直线 BD 向左平移, 使△ DEF 的 顶点 D 与 C 重合,此时 AC 与EF 的关 系还成立吗 ? 请说明理由。变式训练变式三: 如图 (5) , 若把图 (4) 中的△ CEF沿直 线 BC 再向左平移, 使△ CEF 的顶点 C 与 B 重合,此时 AC 与 EF 的关系还 成立吗 ? 请说明理由。变式训练考察的知识点:全等三角形的性质与判定需要用到的知识:等角的余角相等归纳小结2323232323针对练习《课堂导学案》 P41 第 11 题1 、( A 组)如图, D 点在 AB 上, E 点在 AC上, AB=AC, ∠B =∠ C, 求证: AD=AE布置作业2 、( B 组)已知:如图, AB=AC , BD⊥AC , CE⊥AB ,垂足分别为 D 、 E , BD 、 CE 相交于点 F ,求证: ( 1 )△ ABD≌△ACE ( 2 ) BE=CD .布置作业3 、( C 组)在上面例 2 的问题①中 , 连接 AE, 并取 AE 的中点 F ,连接 BF 、 DF ,请判断△ BDF的 形状并证明。布置作业