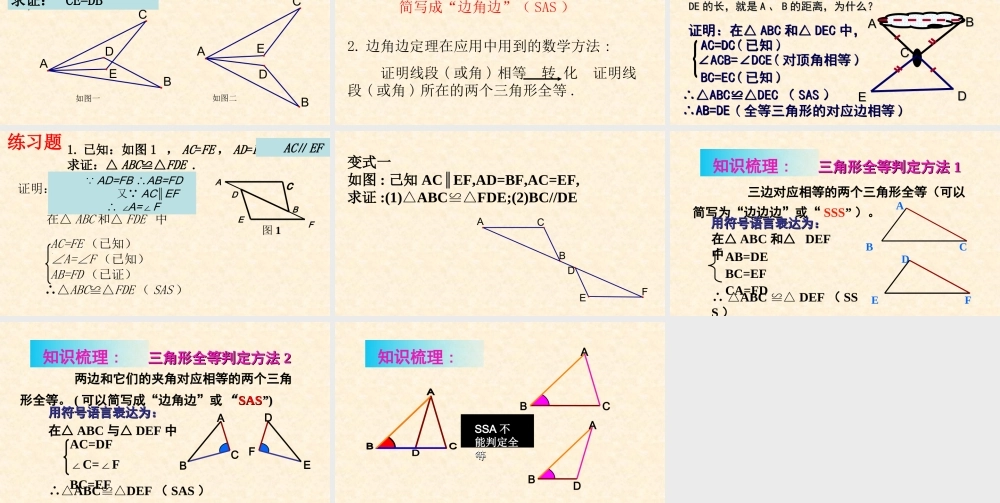
人教版八年级上册 数学§12.2.3 三角形全等的判定南昌市心远中学 胡欣颖 三边对应相等的两个三角形全等(可以简写为“边边边”或“ SSS” )。 三角形全等判定方法 1知识回顾 :除了 SSS 外 , 还有其他情况吗?继续探索三角形全等的条件 .(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有哪几种情况 :SSS不能 !?探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?ABCABC图一图二在图一中, ∠ A是 AB 和 AC 的夹角,符合图一的条件,它可称为“两边夹角”。符合图二的条件, 通常说成“两边和其中一边的对角”已知△ ABC ,画一个△ A′B′C′ 使 A B =A′B′,A C =A′ C ′, ∠A =∠A′ 。结论 : 两边及夹角对应相等的两个三角形全等思考: ① △ A′ B′ C′ 与 △ ABC 全等吗?画法 :1. 画 ∠ DA′ E= ∠A ;2. 在射线 A D 上截取 A′B′=AB,在射线 A′E 上截取 A ′C ′=AC;3. 连接 B ′C′.ACB A′EDCB′′思考: ②这两个三角形全等是满足哪三个条件?探索边角边 三角形全等判定方法三角形全等判定方法 22用符号语言表达为:用符号语言表达为:在△ ABC 与△ DEF 中∴△ABCDEF≌△( SAS ) 两边和它们的夹角对应相等的两个三角形全等。 ( 可以简写成“边角边”或“ “ SASSAS””))FEDCBAAC=DF∠C=F∠BC=EFA45° 探索边边(SSA)BB′C10cm 8cm 8cm 两边及其中一边的对角对应相等的两个三角形全等吗 ?已知: AC=10cm,BC=8cm, ∠A=45 °.△ABC 的形状与大小是唯一确定的吗 ?10cm AB′C45° 8cm 探索边边角 (SSA)BA8cm 45° 10cm CSSA 不存在显然: △ ABC 与△ AB’C 不全等两边及一角对应相等的两个三角形全等吗?① 两边及夹角对应相等的两个三角形全等( SAS) ;② 两边及其中一边的的对角对应相等的两个三角形不一定全等.③ 现在你知道哪些三角形全等的判定方法?SSS, SAS例 1. 如图,在△ AEC 和△ ADB 中,已知 AE=AD , AC=AB ,请说明△ AEC ≌ △ADB 的理由。AE=AD( 已知 )∠A= A( ∠公共角 )AC=AB( 已知 ) ∴ △AECADB≌△( )AEBDCSAS解:在△ AEC 和△ ADB 中变式:如图一,在△ AEC 和△ ADB 中,已知 AE=AD , AC=AB , ∠ CAD=∠BAE 。求证: ∠ C...