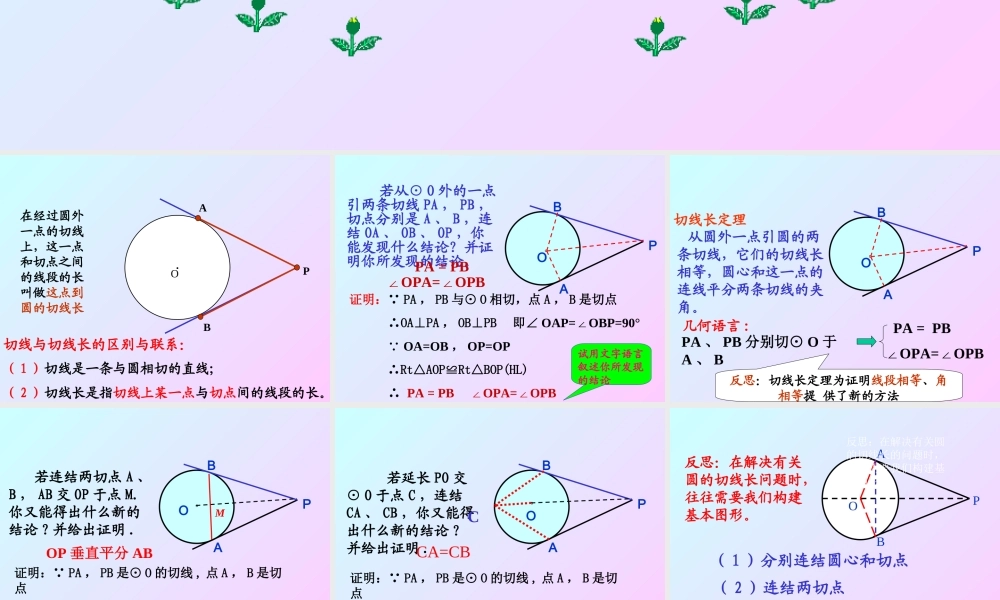
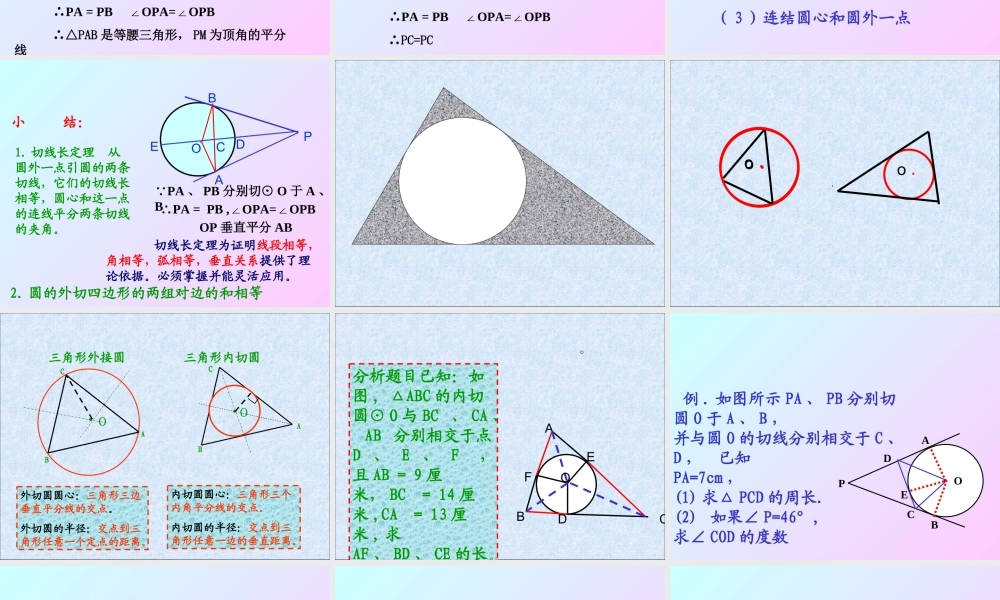
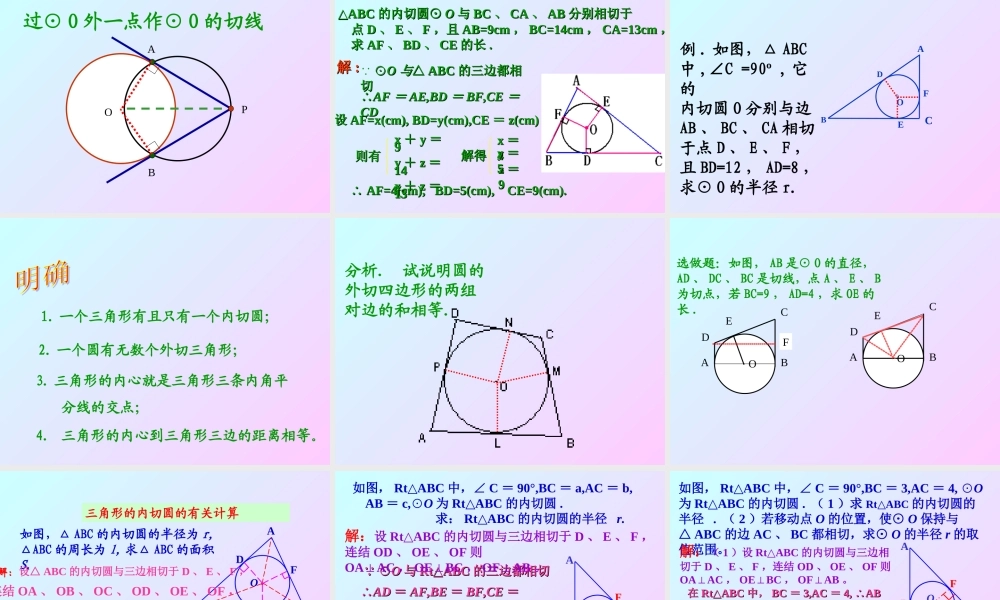
在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长·OPAB切线与切线长的区别与联系:( 1 )切线是一条与圆相切的直线;( 2 )切线长是指切线上某一点与切点间的线段的长。 若从⊙ O 外的一点引两条切线 PA , PB ,切点分别是 A 、 B ,连结 OA 、 OB 、 OP ,你能发现什么结论?并证明你所发现的结论。APO。BPA = PB∠OPA=OPB∠证明: PA , PB 与⊙ O 相切,点 A , B 是切点 ∴OA⊥PA , OB⊥PB 即∠ OAP=OBP=90°∠ OA=OB , OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB OPA=OPB∠∠试用文字语言叙述你所发现的结论PA 、 PB 分别切⊙ O 于A 、 BPA = PB∠OPA=OPB∠ 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理APO。B几何语言 :反思:切线长定理为证明线段相等、角相等提 供了新的方法APO 。BM 若连结两切点 A 、B , AB 交 OP 于点 M.你又能得出什么新的结论 ? 并给出证明 .OP 垂直平分 AB证明: PA , PB 是⊙ O 的切线 , 点 A , B 是切点 ∴PA = PB OPA=OPB∠∠ ∴△PAB 是等腰三角形, PM 为顶角的平分线 ∴OP 垂直平分 ABAPO。B 若延长 PO 交⊙ O 于点 C ,连结CA 、 CB ,你又能得出什么新的结论 ?并给出证明 .CA=CB证明: PA , PB 是⊙ O 的切线 , 点 A , B 是切点 ∴PA = PB OPA=OPB∠∠ ∴PC=PC ∴ △PCA △ PCB △∴AC=BCC。PBAO( 3 )连结圆心和圆外一点( 2 )连结两切点( 1 )分别连结圆心和切点反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形。1. 切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 小 结:APO。BECD PA 、 PB 分别切⊙ O 于 A 、B∴PA = PB ,OPA=OPB∠∠OP 垂直平分 AB 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。2. 圆的外切四边形的两组对边的和相等.o .o .o ..o外切圆圆心:三角形三边垂直平分线的交点。外切圆的半径:交点到三角形任意一个定点的距离。三角形外接圆三角形内切圆.o内切圆圆心:三角形三个内角平分线的交点。内切圆的半径:交点到三角形...