1.2.3简单复合函数的导数VIP免费

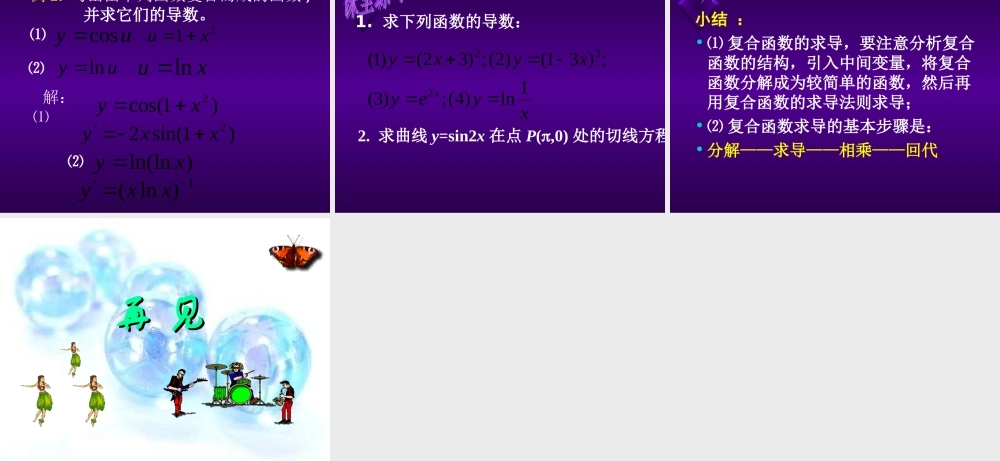
选修 2-2 第 1 章基本求导公式 :知识回顾：)(0,))(1(为常数特殊的：CCkbkx为常数）())(2(1' xx1)0,(ln))(3('aaaaaxx且1),0(ln1)log)(4('aaaxxa且xxsin)(8)(cos ' ))(5('xxeexx1)(6)(ln '  cos)sin)(7('xx根据导数的概念，求函数导数的过程可以用下面的流程图来表示 )(xfy 给定函数 xxfxxfxy）（）（计算 0x )(xAxy  )()(xAxf).()(])()([xgxfxgxf)).((])([为常数CxfCxCf)()()()()(])()([2 xgxgxfxgxfxgxf0)(xg其中法则 1 ：法则 2 ：法则 4 ：法则 3 ：).()()()(])()([xgxfxgxfxgxf复合函数 :)(ufy )(xu 由几个函数复合而成的函数 , 叫复合函数． 由函数与复合而成的函数 一般形式是, u 称为中间变量．)]([xfy高考中所研究的简单复合函数的导数仅限于形如 f (ax+b) 的复合函数 .数学运用数学运用试说明下列函数是怎样复合而成的)21cos()4(;131)3()15ln()2(;)32()1(3xyxyxyxy 求函数的导数 。2(32)yx方法一：22[(32) ](9124)1812xyxxxx问题探究： 2(32)yx2()2uyuu(32)3xuxxuxuyy'''方法二：2yu32ux 看作是函数和函数复合函数，并分别求对应变量的导数如下： 两个导数相乘，得 从而有12183)23(232xxuuyxu将函数； 问题探究： 考察函数的导数 。xy2sinxxxycossin22sin:一方面xxxxxxxxxx2cos2sin2cos2)(cossin2cos)(sin2)cossin2()2(sin22xyxuxuyy'''另一方面：复合函数，并分别求对应变量的导数如下： 两个导数相乘，得 从而有x2cos2xy2sinuysin 看作是函数和函数xu2uuyucos)(sin2)2(xux将函数2)(cosuuyxu分解求导相乘回代建构数学建构数学• 对于一般的复合函数，结论也成立 。• 复合函数的求导法则• 复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数 ，即ayyux ''即：若 y=f(u), u=ax+b ，则xuxuyy'''xuxuyy'''复合函数求导的基本步骤是：(1) 分解(2) 求导(3) 相乘(4) 回代 例 1. 求下列函数的导数：数学运用数学运用)21cos()4(;131)3()15ln()2(;)32()1(3xyxyxyxyuycos21xuuylnxuln)...