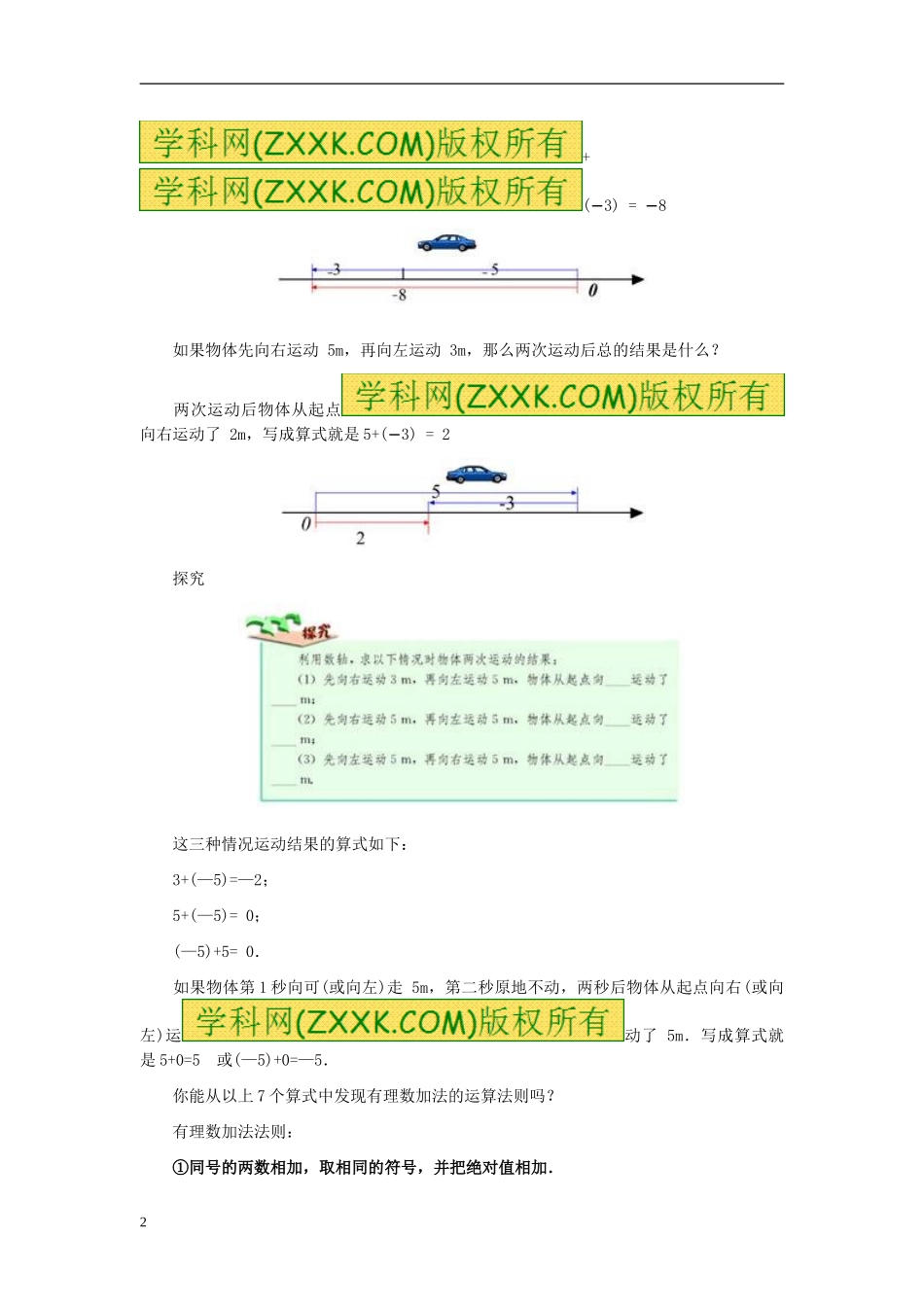
有理数的加减法(一) [本节课内容] 1.有理数的加法 2.有理数的加法的运算律 [本节课学习目标] 1、理解有理数的加法法则. 2、能够应用有理数的加法法则,将有理数的加法转化为非负数的加减运算. 3、掌握异号两数的加法运算的规律. 4、理解有理数的加法的运算律. 5、能够应用有理数的加法的运算律进行计算. [知识讲解] 一、有理数加法: 正有理数及 0 的加法运算,小学已经学过,然而实际问题中做加法运算的数有可能超出正数范围.例如,足球循环赛中,可以把进球数记为正数,失球数记为负数,它们的和叫做净胜球数.如果,红队进4个球,失2个球;蓝队进 1 个球,失 1 个球. 于是红队的净胜球数为 4+(-2),蓝队的净胜球数为 1+(-1). 这里用到正数和负数的加法. 下面借助数轴来讨论有理数的加法. 看下面的问题: 一个物体作左右方向的运动;我们规定向左为负,向右为正,向右运动 5m 记作 5m,向左运动 5m 记作 − 5m;如果物体先向右移动 5m,再向右移动 3m,那么两次运动后总的结果是什么? 两次运动后物体从起点向右移动了 8m,写成算式就是:5+3 = 8 如果物体先向左运动 5m,再向左运动 3m,那么两次运动后总的结果是什么? 两 次 运 动 后 物 体 从 起 点 向 左 运 动 了 8m , 写 成 算 式 就 是 (5)−1+(3) = 8−− 如果物体先向右运动 5m,再向左运动 3m,那么两次运动后总的结果是什么? 两次运动后物体从起点向右运动了 2m,写成算式就是 5+(3) = 2− 探究 这三种情况运动结果的算式如下: 3+(—5)=—2; 5+(—5)= 0; (—5)+5= 0. 如果物体第 1 秒向可(或向左)走 5m,第二秒原地不动,两秒后物体从起点向右(或向左)运动了 5m.写成算式就是 5+0=5 或(—5)+0=—5. 你能从以上 7 个算式中发现有理数加法的运算法则吗? 有理数加法法则: ①同号的两数相加,取相同的符号,并把绝对值相加.2 ②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得零. ③一个数同 0 相加,仍得这个数. 例题 例 1、计算 (-3)+(-9); (2)(-4.7)+3.9. 分析:解此题要利用有理数的加法法则. 解:(1) (-3)+(-9)=-(3+9)=-12 (2) (-4.7)+3·9=-(4.7-3.9)=-0.8. 例 2 足球循环赛中,红队胜黄队 4:1,黄队胜蓝队 1:0,蓝队胜红队 1:0,计...