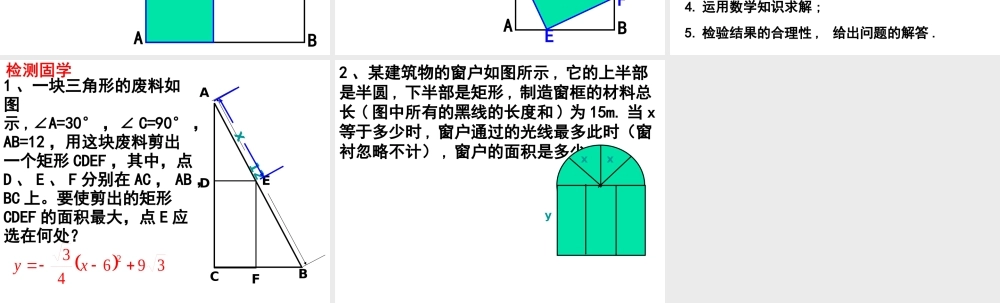
实际问题与二次函数( 2)— 面积问题保康县熊绎中学九年级数学备课组探究 2 :用总长为 60m 的篱笆围成矩形场地,矩形面积 s 随矩形一边长 l 的变化而变化,( 1 )写出面积 s 与一边长 l 之间的函数关系式,并写出自变量的取值范围。( 2 )画出函数的大致图像。( 3 )当 l 是多少时,场地的面积 s 最大?合作互学1 、星光中学课外活动小组准备围建一个矩形生物苗圃园.其中一边靠墙,另外三边用长为 30 米的篱笆围成.已知墙长为 18 米 ( 如图 ) ,设这个苗圃园垂直于墙的一边的长为 x 米.(2) 垂直于墙的一边的长为多少米时,这个苗圃园的面积最大?并求出这个最大值;(1) 若平行于墙的一边的长为 y 米,直接写出 y 与x 之间的函数关系式及其自变量 x 的取值范围;(3) 当这个苗圃园的面积不小于 88 平方米时,试结合函数图象,直接写出 x 的取值范围.变式探究2. 用 48 米长的竹篱笆围建一矩形养鸡场 ,养鸡场一面用砖砌成 , 另三面用竹篱笆围成 , 并且在与砖墙相对的一面开 2 米宽的门( 不用篱笆 ), 问养鸡场的边长为多少米时 ,养鸡场占地面积最大 ? 最大面积是多少 ? 2mym2xmxm例 2 如图,从一张矩形纸较短的边上找一点 E ,过 E 点剪下两个正方形,它们的边长分别是 AE , DE 。要使剪下的面积最小,点E 应选在何处?为什么?ABCDEx变式:如图 , 点 E 、 F 、 G 、 H 分别位于正方形 ABCD 的四条边上,四边形 EFGH 也是正方形,当点 E 位于何处时,正方形 EFGH 的面积最小?ABCDHEFG1. 理解问题 ;“ 二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?2. 分析问题中的变量和常量 , 以及它们之间的关系 ;3. 用数学的方式表示出它们之间的关系 ;4. 运用数学知识求解 ;5. 检验结果的合理性 , 给出问题的解答 .小结评学1 、一块三角形的废料如图示 ,∠A=30° ,∠ C=90° ,AB=12 ,用这块废料剪出一个矩形 CDEF ,其中,点D 、 E 、 F 分别在 AC , AB ,BC 上。要使剪出的矩形CDEF 的面积最大,点 E 应选在何处? 12ABCEFD x396432 xy2 、某建筑物的窗户如图所示 , 它的上半部是半圆 , 下半部是矩形 , 制造窗框的材料总长 ( 图中所有的黑线的长度和 ) 为 15m. 当 x等于多少时 , 窗户通过的光线最多此时(窗衬忽略不计) , 窗户的面积是多少 ?xxy