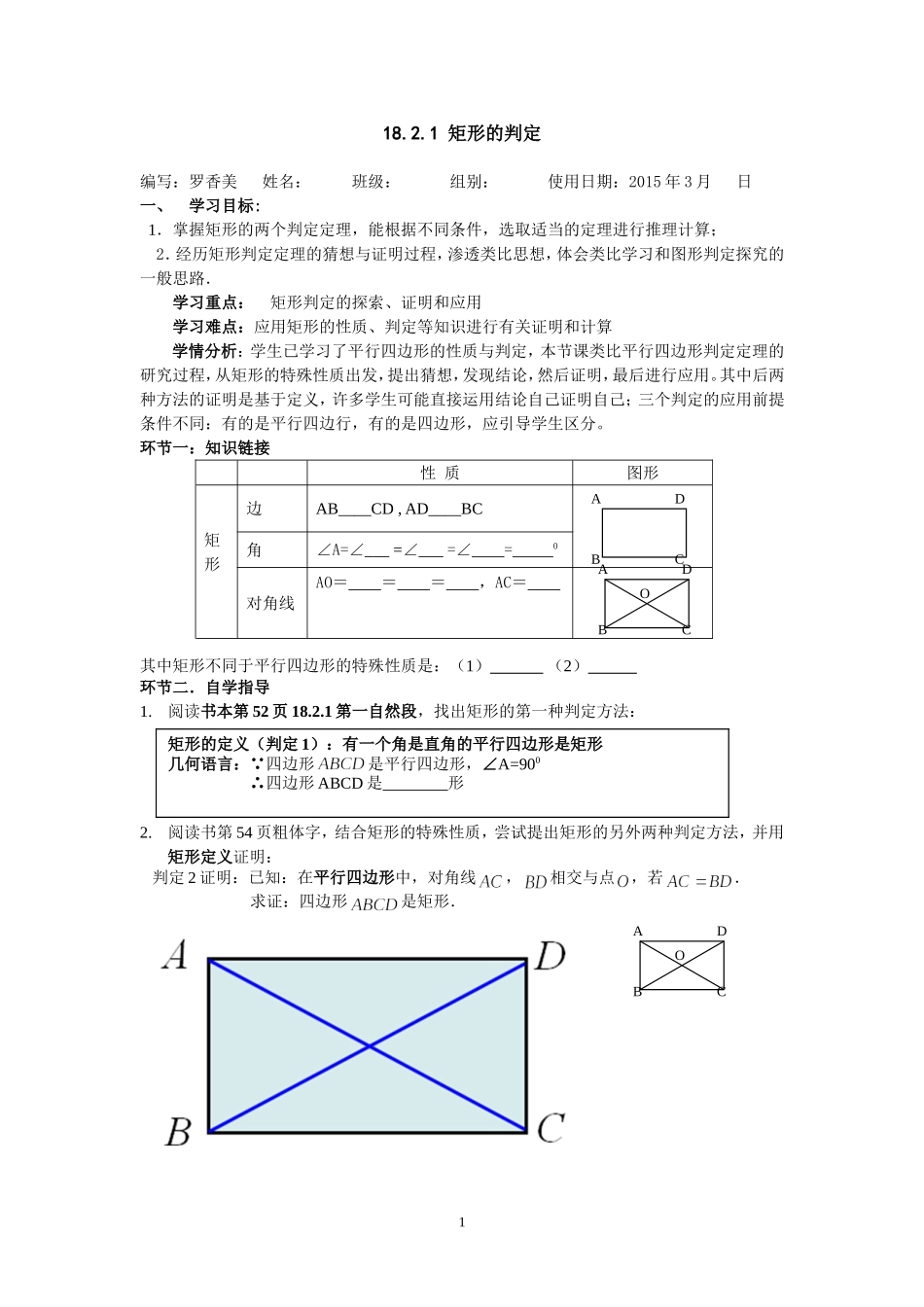
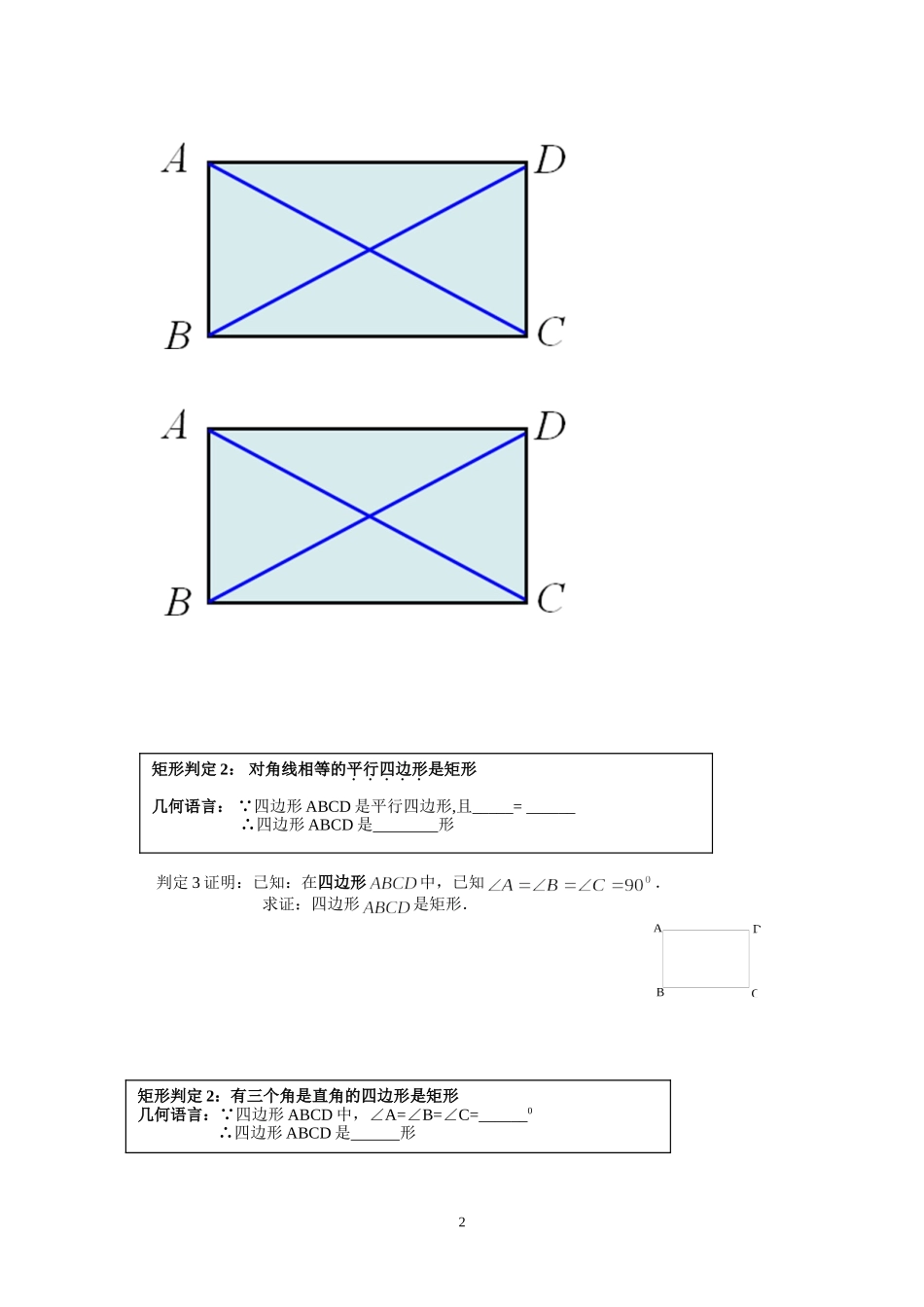
18.2.1 矩形的判定编写:罗香美 姓名: 班级: 组别: 使用日期:2015 年 3 月 日 一、 学习目标: 1.掌握矩形的两个判定定理,能根据不同条件,选取适当的定理进行推理计算; 2.经历矩形判定定理的猜想与证明过程,渗透类比思想,体会类比学习和图形判定探究的一般思路. 学习重点: 矩形判定的探索、证明和应用 学习难点:应用矩形的性质、判定等知识进行有关证明和计算学情分析:学生已学习了平行四边形的性质与判定,本节课类比平行四边形判定定理的研究过程,从矩形的特殊性质出发,提出猜想,发现结论,然后证明,最后进行应用。其中后两种方法的证明是基于定义,许多学生可能直接运用结论自己证明自己;三个判定的应用前提条件不同:有的是平行四边行,有的是四边形,应引导学生区分。环节一:知识链接性 质图形矩形边AB____CD , AD____BC角∠A=∠___ =∠___ =∠ = 0对角线AO= = = ,AC= 其中矩形不同于平行四边形的特殊性质是:(1) (2) 环节二.自学指导1.阅读书本第 52 页 18.2.1 第一自然段,找出矩形的第一种判定方法:2.阅读书第 54 页粗体字,结合矩形的特殊性质,尝试提出矩形的另外两种判定方法,并用矩形定义证明: 判定 2 证明:已知:在平行四边形中,对角线,相交与点,若. 求证:四边形是矩形.1矩形的定义(判定 1):有一个角是直角的平行四边形是矩形几何语言: 四边形是平行四边形,∠A=900 ∴四边形 ABCD 是 形ABDCABDCOABDCODCBA 判定 3 证明:已知:在四边形中,已知. 求证:四边形是矩形.2矩形判定 2: 对角线相等的平行四边形是矩形几何语言: 四边形 ABCD 是平行四边形,且_____= ______∴四边形 ABCD 是 形矩形判定 2:有三个角是直角的四边形是矩形几何语言: 四边形 ABCD 中,∠A=∠B=∠C=______0 ∴四边形 ABCD 是 形EDCBA小结:矩形的判定方法:(1)定义判定:有一个角是_________的平行四边形是矩形(2)对角线_________的平行四边形是矩形(3)有三个角是________的四边形是矩形环节三、基础练习:1、判断一个四边形是矩形的方法有 (填序号)(1) 一个角是直角 (2)对角线垂直 (3)对角线互相平分且相等 (4)三个角是直角2、判断一个平行四边形是矩形的方法有 (填序号)(1) 一个是直角 (2) 对角线垂直 (3)对角线互相平分 (4)对角线相等3、工人师傅在做门框或矩形零件时,常用测量平行四边形的两...