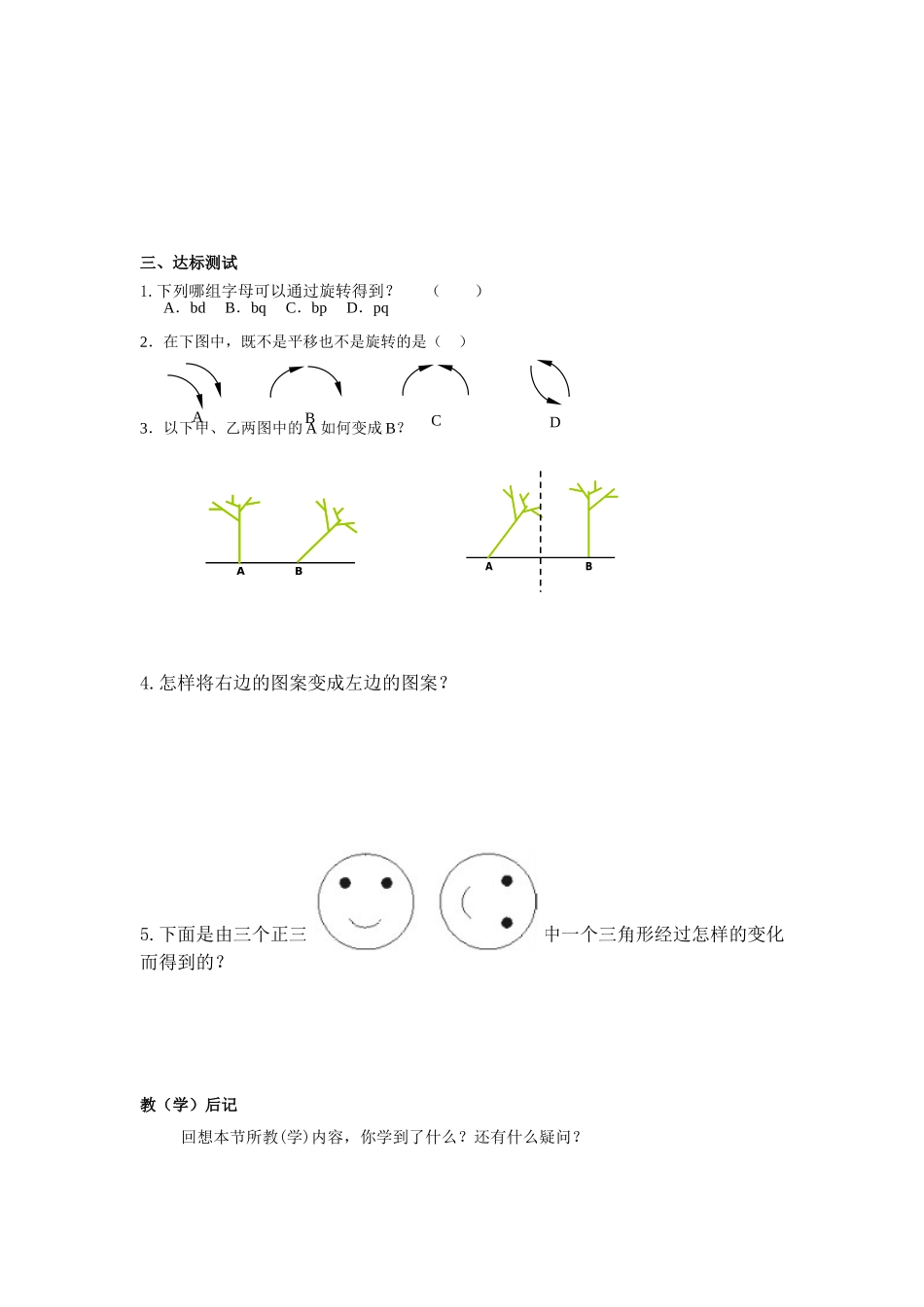
8.5 平面图形的全等变换学习目标: 1. 经历探索图形之间的变换关系的过程.发展对一般图形的分析能力,化归意识. 2. 提高综合运用变换解决问题的能力.学习过程:一、自主学习1.图形之间的变换关系的基本类型有: 、 、 .2.平移、旋转、轴对称的区别是:(1)变换的 不同;(2)对应点连线的 不同;(3)三种变换所需的 不同.3.三种变换的联系是:三种变换都是平面内的变换,都是不改变图形的 和 ,只改变图形的 .二、探究学习探究 1. 图形之间的三种基本变换1.如图是由四部分组成的,每部分都包括两个小“十字”.(1)找出图中的“基本图案”,并说明该“基本图案”可以经过怎样的变换得到 8--31.(2)如果把右边两个作为“基本图案”,他它能经过适当的旋转得到其他部分吗?经过平移呢?(3)右边的两个能通过作轴对称图形得到图吗?(4)你还能用其他的方法,通过图中的“基本图案”得到图吗?探究 2. 轴对称、平移、旋转三种变换的组合变换1.怎样将图中的甲图案通过变换与乙图案重合? 三、达标测试1.下列哪组字母可以通过旋转得到? ( )A.bd B.bq C.bp D.pq2.在下图中,既不是平移也不是旋转的是( )3.以下甲、乙两图中的 A 如何变成 B?4.怎样将右边的图案变成左边的图案?5.下面是由三个正三角形拼成的,它可以看做由其中一个三角形经过怎样的变化而得到的?教(学)后记回想本节所教(学)内容,你学到了什么?还有什么疑问?ABCDABAB四、课后作业1.把△ABC 旋转 1800得到△A1B1C1,再把△A1B1C1作轴对称变换得到△A2B2C2,则△ABC 和△A1B1C1之间( )A.有全等关系 B.无全等关系C.可能有全等关系 D.以上都不对2. 把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图 1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图 2)的对应点所具有的性质是( )A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分 C.对应点连线被对称轴垂直平分 D.对应点连线互相平行 3.已知如图 1 所示的四张牌,若将其中一张牌旋转180后得到图 2,则旋转的牌是( )4.如图,把一张长方形纸片对折,折痕为 AB,再以 AB 的 中点 O 为顶点把平角∠AOB 三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以 O 为顶点的等腰三角形...