47新课标高一数学正弦定理VIP免费

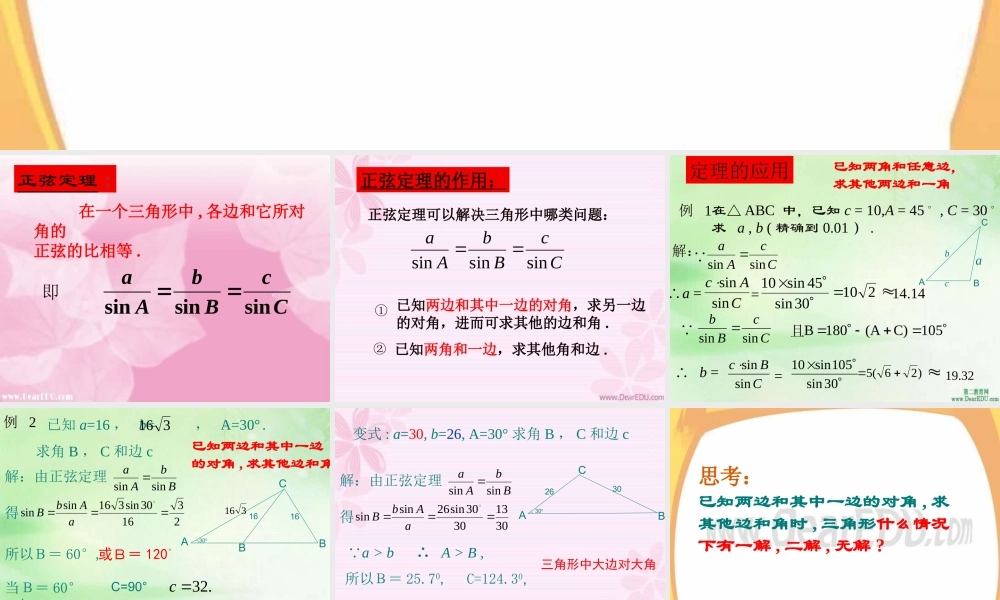
正弦定理正弦定理 : 在一个三角形中 , 各边和它所对角的正弦的比相等 .CcBbAasinsinsin即正弦定理的作用：正弦定理可以解决三角形中哪类问题： ①已知两角和一边，求其他角和边 . ②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角 .CcBbAasinsinsin定理的应用例 1在△ ABC 中，已知 c = 10,A = 45。 , C = 30。求 a , b ( 精确到 0.01 ） .解： 且 105C)(A180 B CcBbsinsin∴ b = CBcsinsin 19.32=30sin105sin10已知两角和任意边，求其他两边和一角CcAasinsin ∴a = CAcsinsin14.14=21030sin45sin10BACbc)26(5a例 2 已知 a=16 ， b= ， A=30° .求角 B ， C 和边 c已知两边和其中一边的对角 , 求其他边和角解：由正弦定理BbAasinsin得231630sin316sinsinaAbB所以Ｂ＝ 60°,或Ｂ＝ 120°当 时Ｂ＝ 60°C=90°.32cC=30°.16sinsinACac316当Ｂ＝ 120° 时B16300ABC16316变式 : a=30, b=26, A=30° 求角 B ， C 和边 c300ABC2630解：由正弦定理BbAasinsin得30133030sin26sinsinaAbB所以Ｂ＝ 25.70,C=124.30,57.49sinsinACac a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角 , 求其他边和角时 , 三角形什么情况下有一解 , 二解 , 无解 ?思考：ACabab 一解练习： P9 1 、 2 、 3cosA cosB cosC例 3 ：试判断△ ABC 的形状。ACBD例 4实际问题例 1 、如图，要测底部不能到达的烟囱的高 AB ，从与烟囱底部在同一水平直线上的 C 、 D 两处，测得烟囱的仰角分别是和4560， CD 间的距离是 12m. 已知测角仪器高 1.5m, 求烟囱的高。图中给出了怎样的一个几何图形？已知什么，求什么？想一想实例讲解AA1BCDC1D1分析：如图，因为 AB=AA1+A1B ，又已知 AA1=1.5m, 所以只要求出 A1B 即可。解：15sin120sin12sinsinsinsin:,154560,111111111111BDDCBCDBCBDCBDCDBC由正弦定理可得中在662184.2836182211BCBA)(9.295.14.2811mAABAAB答：烟囱的高为 29.9m.ABCDE652035ABCDE652035BEDC2.57,1.89,2.01,45...