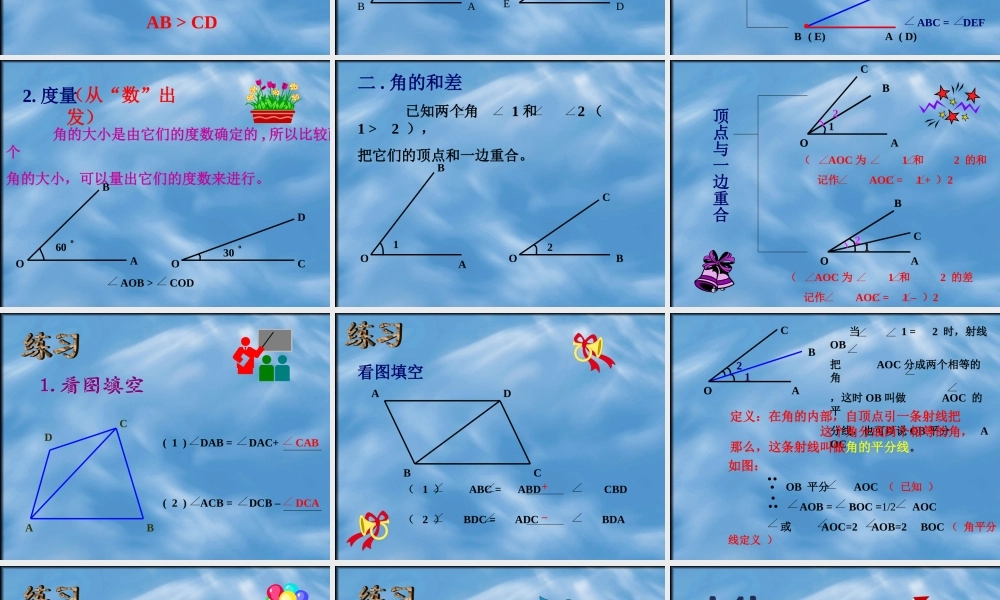
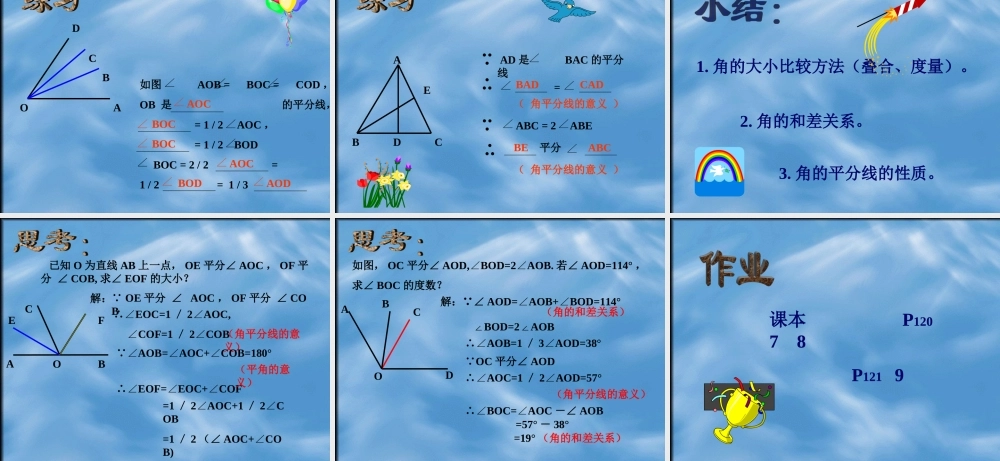
梁建柳制作人: 1. 根据图形会比较角的大小 2. 理解角的和差概念 3. 掌握角平分线的概念 线段的比较方法1. 从“形”出发,利用线段移动叠合 的方法 ABAC2. 以“数” 出发,通过度量长度进行 数值大 小比较。 经过叠合A( C )ACABCAABAB( AB > AC )( AB = AC )( AB < AC ) 以“数” 出发,通过度量长度进行 数值大 小比较。二、 度量5 CMAB3 CMC DAB > CD 一、叠合 ( 从“形”出发)( 1 )以知 ABC 与 DEF 如图:DEFABC ABCF( E) ( D)ABC( E) ( D)( F )ABCF( E )( D )经过叠合 ABC> DEFAB C< DEFABC = DEF 2. 度量 角的大小是由它们的度数确定的 , 所以比较两个角的大小,可以量出它们的度数来进行。60 。AOB30 。CODAOB > COD(从“数”出发) 二 . 角的和差 已知两个角 1 和 2 ( 1 > 2 ),把它们的顶点和一边重合。12AOBBOC 1OAB2CBOA1BOBC2 AOC 为 1 和 2 的和 记作 AOC = 1 + 2() AOC 为 1 和 2 的差 记作 AOC = 1 – 2()顶点与一边重合 ABDC( 1 ) DAB = DAC+ ( 2 ) ACB = DCB –CABDCA 看图填空( 1 ) ABC = ABD CBD( 2 ) BDC = ADC BDA ABDC+– 2121BOACO 当 1 = 2 时,射线OB把 AOC 分成两个相等的角,这时 OB 叫做 AOC 的平分线,也可以说 OB 平分 AOC定义:在角的内部,自顶点引一条射线把 这个角分成两个相等的角,那么,这条射线叫做角的平分线。 如图: OB 平分 AOC ( 已知 ) AOB = BOC =1/2 AOC 或 AOC=2 AOB=2 BOC ( 角平分线定义 ) ABCDO如图 AOB = BOC = COD ,OB 是 的平分线, = 1 / 2 AOC , = 1 / 2 BOD BOC = 2 / 2 =1 / 2 = 1 / 3AOCBOCBOCAOCBODAOD ABCDE AD 是 BAC 的平分线=ABC = 2 ABE平分( 角平分线的意义 )BADCADBEABC( 角平分线的意义 ) 1. 角的大小比较方法(叠合、度量)。2. 角的和差关系。3. 角的平分线的性质。 已知 O 为直线 AB 上一点, OE 平分∠ AOC , OF 平分 ∠ COB, 求∠ EOF 的大小?解: ∵ OE 平分 ∠ AOC , OF 平分 ∠ COB∴∠EOF=EOC+COF∠∠=1 / 2AOC+1∠/ 2C∠OB=1 / 2 (∠ AOC+CO∠B)=90°∴∠EOC=1 / 2AOC,∠ ∠COF=1 / 2COB∠(角平分线的意义)∵∠AOB=AOC+COB=180°∠∠(平角的意义)ABECFO 如图, OC 平分∠ AOD,BOD=2AOB.∠∠若∠ AOD=114° ,求∠ BOC 的度数?ABCDO解:∵∠ AOD=AOB+BOD=114°∠∠∴∠AOB=1 / 3AOD=38°∠∵OC 平分∠ AOD∴∠AOC=1 / 2AOD=57°∠(角平分线的意义)∴∠BOC=AOC∠-∠ AOB(角的和差关系)∠BOD=2AOB∠=57° - 38°=19° (角的和差关系) 课本 P120 7 8 P121 9