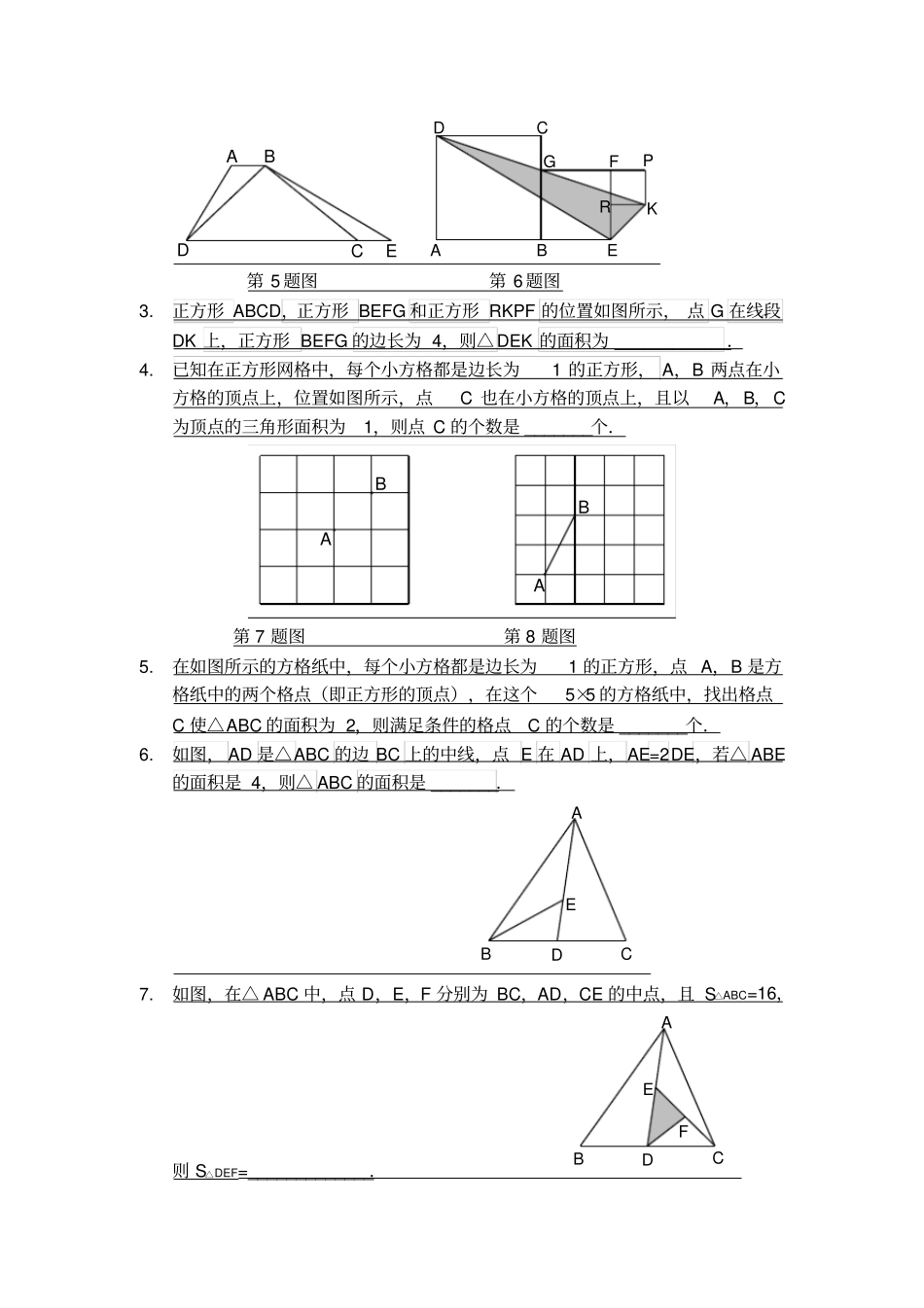
专题:在三角形中巧用面积法解题(一)证明面积问题常用的理论依据 1. 三角形的中线把三角形分成两个面积相等的部分。 2. 同底同高或等底等高的两个三角形面积相等。 3. 平行四边形的对角线把其分成两个面积相等的部分。 4. 同底(等底)的两个三角形面积的比等于高的比。同高(或等高)的两个三角形面积的比等于底的比。 5. 三角形的面积等于等底等高的平行四边形的面积的一半。(二)证明面积问题常用的证题思路和方法 1. 分解法:通常把一个复杂的图形,分解成几个三角形。 2. 作平行线法:通过平行线找出同高(或等高)的三角形。 3. 利用有关性质法:比如利用中点、中位线等的性质。 4. 还可以利用面积解决其它问题。一、利用面积自身相等的性质解题例 1 如图,在直角三角形ABC中, AB=13,AC=12,BC=5,求 AB边上的高 AD的长。CABD。例 3 如图, 由图中已知的小三角形的面积的数据,可得ABC 的面积为。FEDCBAO25353040小结 :我们知道等底等高的两三角形的面积相等,等底不等高的两三角形面积的比等于其对应高的比,等高而不等底的两三角形面积的比等于其对应底的比。三、利用面积的可分性解题例4 如 图 , 已 知 等 边 三 角ABC , P为ABC 内 一 点 , 过P作,,,PDBC PEAC PFABABC的 高 为h.试 说 明PDPEPFh 。ABCDPFE小结 :用面积的可分性解题,一般要将图形分成若干个小三角形,利用其整体等于部分之和建立关于条件和结论的关系式,从而方便快捷地解决问题。练习:1、如图,已知ABC 和BDC ,AC与 BD交于点o,且直线AD∥BC,图中四个小三角形 的 面 积 分 别 为1S 、2S 、3S 、4S , 试 判 断2S 和4S 的 大 小 关 系 , 并 说 明 理 由 。DBAOCS4S3S1S22、如图,四边形 ABCD中,对角线 BD上有一点 O,OB:OD=3:2, S AOB =6, S COD =1,试求 S AOD 与 S BOC 的面积比。DACBO3、 如图, P 是等腰三角形ABC底边 BC上的任一点,PEAB 于 E, PFAC 于 F,BH 是等腰三角形AC边上的高。猜想:PE、PF 和 BH间具有怎样的数量关系?ABCpEFH1.如图,在正方形 ABCD 中, BC=2,∠DCE 是正方形 ABCD 的外角, P 是∠DCE 的平分线 CF 上任意一点,则△ PBD 的面积等于 _________.FECDBAP2.如图,在梯形 ABCD 中,AB∥CD,延长 DC 到 E,使 CE=AB,连接 BD,BE.若梯形 ABCD 的面积为 25cm2,则△ BDE 的面积为 ___...