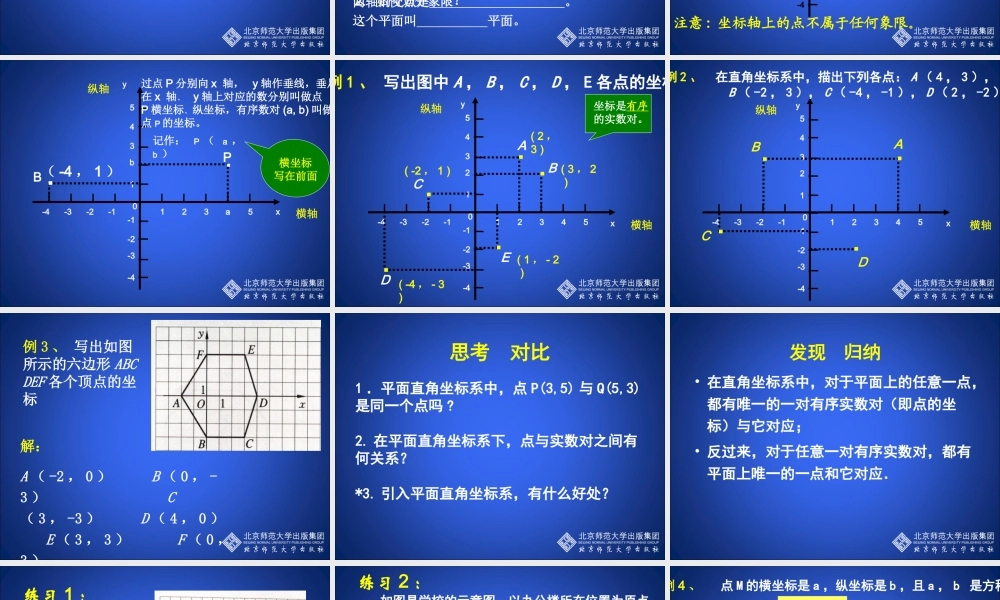
第三章 位置与坐标2. 平面直角坐标系(第 1 课时)什么是数轴? 规定了原点、正方向、单位长度的直线就构成了数轴。回顾与思考·单位长度01234-3-2-1原点 数轴上的点 A 表示数 1. 反过来,数 1 就是点 A 的位置。我们说点 1 是点 A 在数轴上的坐标。 同理可知,点 B 在数轴上的坐标是 -3 ;点 C在数轴上的坐标是 2.5 ;点 D 在数轴上坐标是 0.数轴上的点与实数之间存在着一一对应的关系。数轴上的点与实数之间存在着一一对应的关系。0123-1-2-3CADB 如果课上老师要点一名同学回答问题,但不知道同学们的姓名,我想根据同学们所在的位置来确定,你能帮我解决吗?我帮老师解决问题 讲 台胡天宇列行123462841050阅读教材,回答下列问题:1. 平面内 组成平面直角坐标系, 叫 x 轴(横轴),取向 为正方向, 叫 y轴(纵轴),取向 为正方向。两轴的交点是 。这个平面叫 平面。2. 如何划分象限? 两条互相垂直且有公共原点的数轴水平的数轴右上铅直的数轴原点坐标012345-4-3-2-1x横轴原点第一象限第四象限第三象限第二象限注意 : 坐标轴上的点不属于任何象限。31425-2-4-1-3y纵轴·P314b5-2-4-1-30123a5-4-3-2-1x横轴y纵轴过点 P 分别向 x 轴, y 轴作垂线,垂足在 x 轴﹑ y 轴上对应的数分别叫做点P 横坐标﹑纵坐标,有序数对 (a, b) 叫做点 P 的坐标。记作: P ( a , b )横坐标写在前面·B( -4 , 1 )·B31425-2-4-1-3012345-4-3-2-1x横轴y纵轴·C·A·E·D( 2 ,3 )( 3 , 2 )( -2 , 1 )( -4 , - 3 )( 1 , - 2 )坐标是有序的实数对。例 1 、 写出图中 A , B , C , D , E 各点的坐标。31425-2-4-1-3012345-4-3-2-1x横轴y纵轴·B·A·D·C例 2 、 在直角坐标系中,描出下列各点: A ( 4 , 3 ), B ( -2 , 3 ), C ( -4 , -1 ), D ( 2 , -2 )。例 3 、 写出如图所示的六边形 ABCDEF 各个顶点的坐标解:A ( -2 , 0 ) B ( 0 , -3 ) C( 3 , -3 ) D ( 4 , 0 ) E ( 3 , 3 ) F ( 0 ,3 )1 .平面直角坐标系中,点 P(3,5) 与 Q(5,3)是同一个点吗 ?2. 在平面直角坐标系下,点与实数对之间有何关系?*3. 引入平面直角坐标系,有什么好处?思考 对比发现 归纳• 在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实...