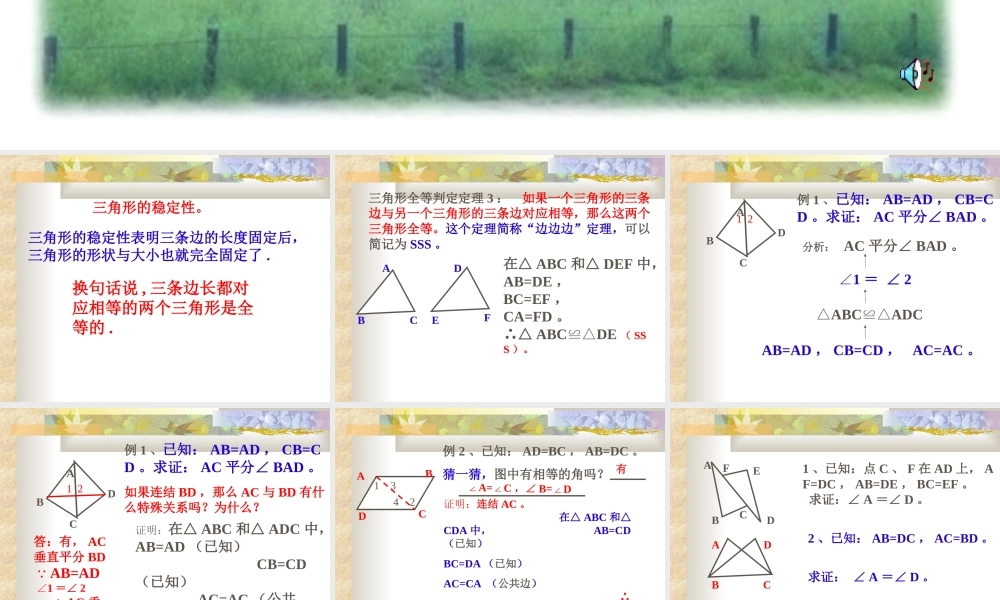
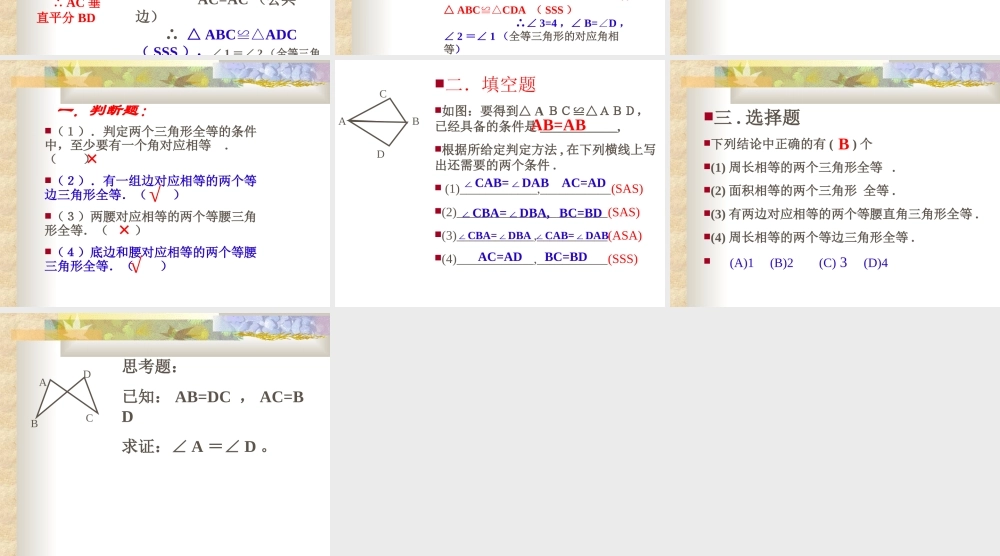
三角形的稳定性。三角形的稳定性表明三条边的长度固定后,三角形的形状与大小也就完全固定了 .换句话说 , 三条边长都对应相等的两个三角形是全等的 . 三角形全等判定定理 3 : 如果一个三角形的三条边与另一个三角形的三条边对应相等,那么这两个三角形全等。这个定理简称“边边边”定理,可以简记为 SSS 。ABCDEF在△ ABC 和△ DEF 中,AB=DE ,BC=EF ,CA=FD 。∴△ ABCDE≌△( SSS )。 例 1 、已知: AB=AD , CB=CD 。求证: AC 平分∠ BAD 。 ABCD1 2分析: AC 平分∠ BAD 。 ∠1 = ∠ 2 △ABCADC ≌△AB=AD , CB=CD , AC=AC 。 ABCD1 2例 1 、已知: AB=AD , CB=CD 。求证: AC 平分∠ BAD 。证明:在△ ABC 和△ ADC 中,AB=AD (已知) CB=CD(已知) AC=AC (公共边) ∴ △ ABCADC≌△( SSS ),∠ 1 =∠ 2 (全等三角形的对应角相等) AC 平分∠ BAD (角平分线的定义)。 如果连结 BD ,那么 AC 与 BD 有什么特殊关系吗?为什么?答:有, AC垂直平分 BD ∵ AB=AD 1∠ =∠ 2 ∴ AC 垂直平分 BD 例 2 、已知: AD=BC , AB=DC 。猜一猜,图中有相等的角吗? A BD C∠A=C∠,∠ B=D∠证明:连结 AC 。 在△ ABC 和△CDA 中, AB=CD(已知)BC=DA (已知)AC=CA (公共边) ∴ △ ABCCDA ≌△( SSS ) ∴∠ 3=4 ,∠ B=D∠,∠ 2 =∠ 1 (全等三角形的对应角相等)∴∠1+3=2+4∠∠∠ ,即∠ BAD=BCD∠。1 34 2有 1 、已知:点 C 、 F 在 AD 上, AF=DC , AB=DE , BC=EF 。 求证:∠ A =∠ D 。2 、已知: AB=DC , AC=BD 。 求证: ∠ A =∠ D 。AFBCDEA DB C 一.判断题:(1).判定两个三角形全等的条件中,至少要有一个角对应相等 .( )(2).有一组边对应相等的两个等边三角形全等.( )(3)两腰对应相等的两个等腰三角形全等.( )(4)底边和腰对应相等的两个等腰三角形全等.( )×√×√二.填空题如图:要得到△ А BC≌△ABD,已经具备的条件是 ____________,根据所给定判定方法 , 在下列横线上写出还需要的两个条件 . (1)____________,___________(SAS)(2)____________,___________(SAS)(3)____________,___________(ASA)(4)____________,___________(SSS)A B CDAB=AB∠CAB=DAB AC=AD∠∠CBA=DBA, BC=BD∠∠CBA=DBA CAB=DAB∠∠∠ AC=AD BC=BD 三 . 选择题下列结论中正确的有 ( ) 个(1) 周长相等的两个三角形全等 .(2) 面积相等的两个三角形 全等 .(3) 有两边对应相等的两个等腰直角三角形全等 .(4) 周长相等的两个等边三角形全等 . (A)1 (B)2 (C) 3 (D)4B 思考题:已知: AB=DC , AC=BD求证:∠ A =∠ D 。ADBC