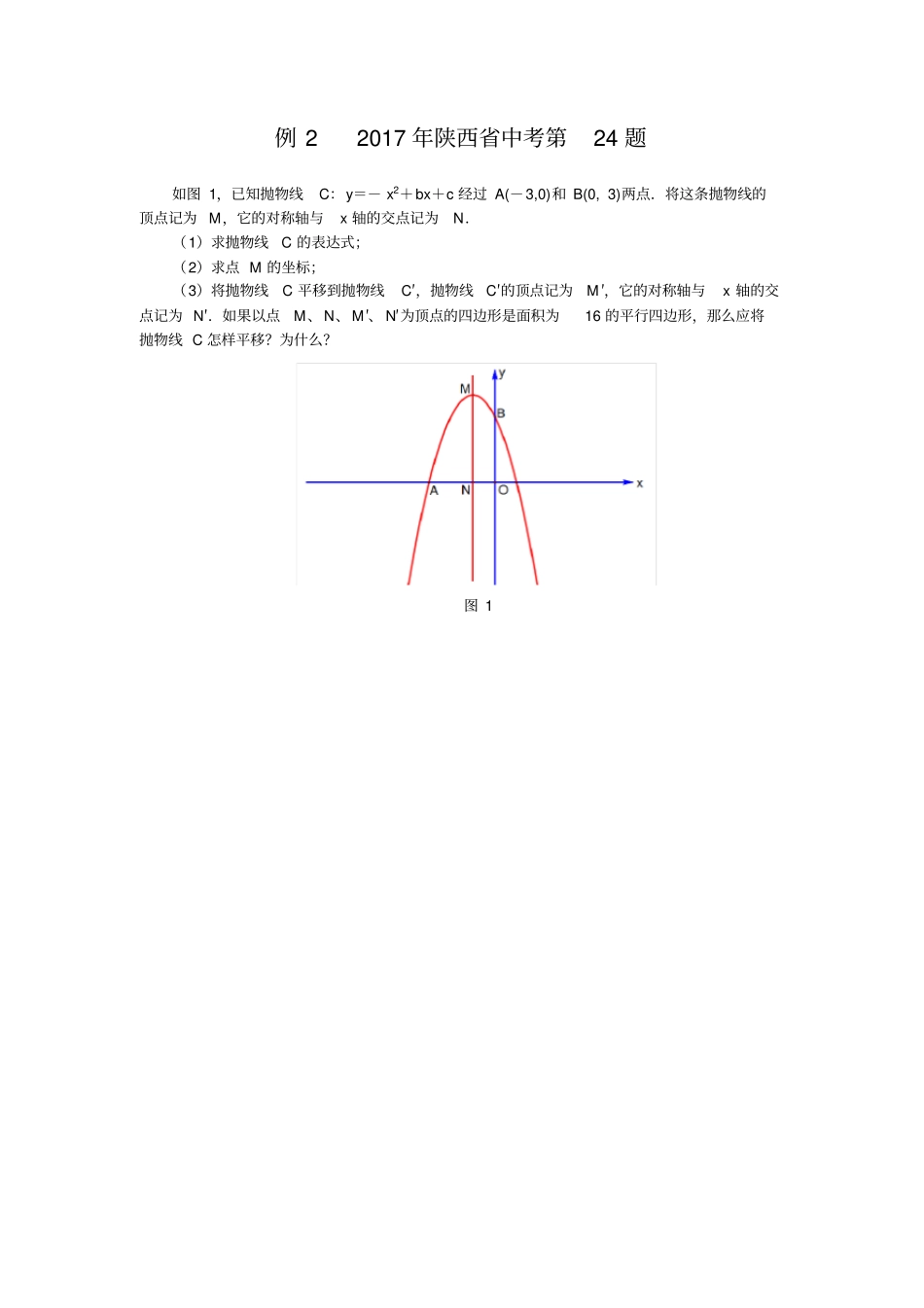
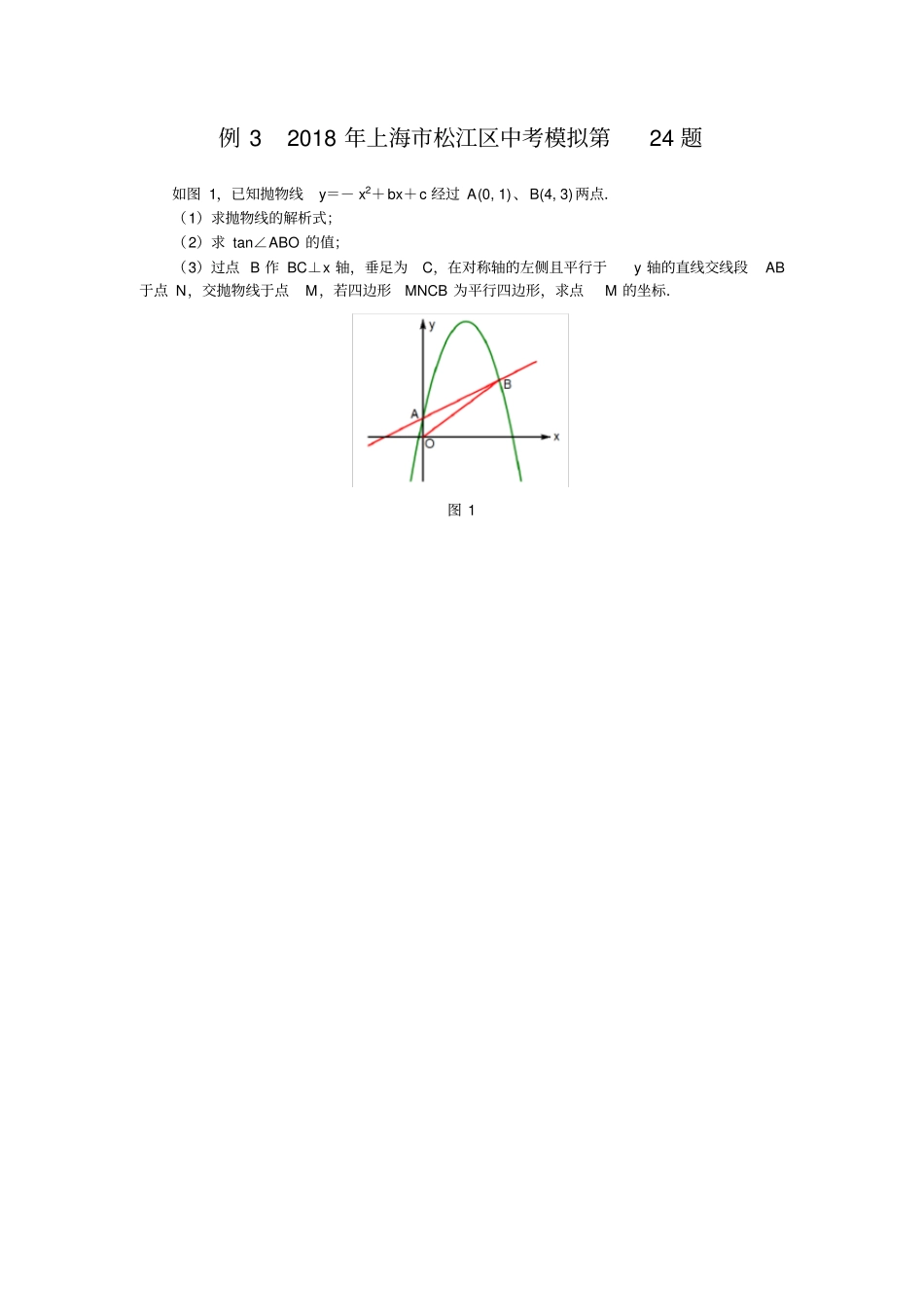
1.4 因动点产生的平行四边形问题例 1 2017 年成都市 中考第 28 题如图 1,在平面直角坐标系中,抛物线y= ax2-2ax-3a(a<0)与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),经过点 A 的直线 l:y=kx+b 与 y 轴负半轴交于点C,与抛物线的另一个交点为D,且 CD=4AC.(1)直接写出点A 的坐标,并求直线l 的函数表达式(其中k、b 用含 a 的式子表示) ;(2)点 E 是直线 l 上方的抛物线上的动点,若△ ACE 的面积的最大值为54 ,求 a 的值;(3)设 P 是抛物线的对称轴上的一点,点Q 在抛物线上,以点A、D、P、Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标;若不能,请说明理由.图 1 备用图例 2 2017 年陕西省中考第24 题如图 1,已知抛物线C:y=- x2+bx+c 经过 A(-3,0)和 B(0, 3)两点.将这条抛物线的顶点记为 M,它的对称轴与x 轴的交点记为N.(1)求抛物线C 的表达式;(2)求点 M 的坐标;(3)将抛物线C 平移到抛物线C′,抛物线C′的顶点记为M ′,它的对称轴与x 轴的交点记为 N′.如果以点M、N、M′、 N′为顶点的四边形是面积为16 的平行四边形,那么应将抛物线 C 怎样平移?为什么?图 1 例 3 2018 年上海市松江区中考模拟第24 题如图 1,已知抛物线y=- x2+bx+c 经过 A(0, 1)、B(4, 3)两点.(1)求抛物线的解析式;(2)求 tan∠ABO 的值;(3)过点 B 作 BC⊥x 轴,垂足为C,在对称轴的左侧且平行于y 轴的直线交线段AB于点 N,交抛物线于点M,若四边形MNCB 为平行四边形,求点M 的坐标.图 1 例 4 2017 年福州市中考第21 题如图 1,在 Rt△ ABC 中,∠ C=90° ,AC= 6,BC=8,动点 P 从点 A 开始沿边 AC 向点C 以每秒 1 个单位长度的速度运动,动点Q 从点 C 开始沿边CB 向点 B 以每秒 2 个单位长度的速度运动,过点P 作 PD//BC,交 AB 于点 D,联结 PQ.点 P、Q 分别从点 A、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒( t≥0).(1)直接用含t 的代数式分别表示:QB= _______,PD=_______ ;(2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值;若不存在,说明理由,并探究如何改变点Q 的速度(匀速运动) ,使四边形 PDBQ 在某一时刻为菱形,求点Q的速度;(3)如图 2,在整个运动过程中,求出线段...