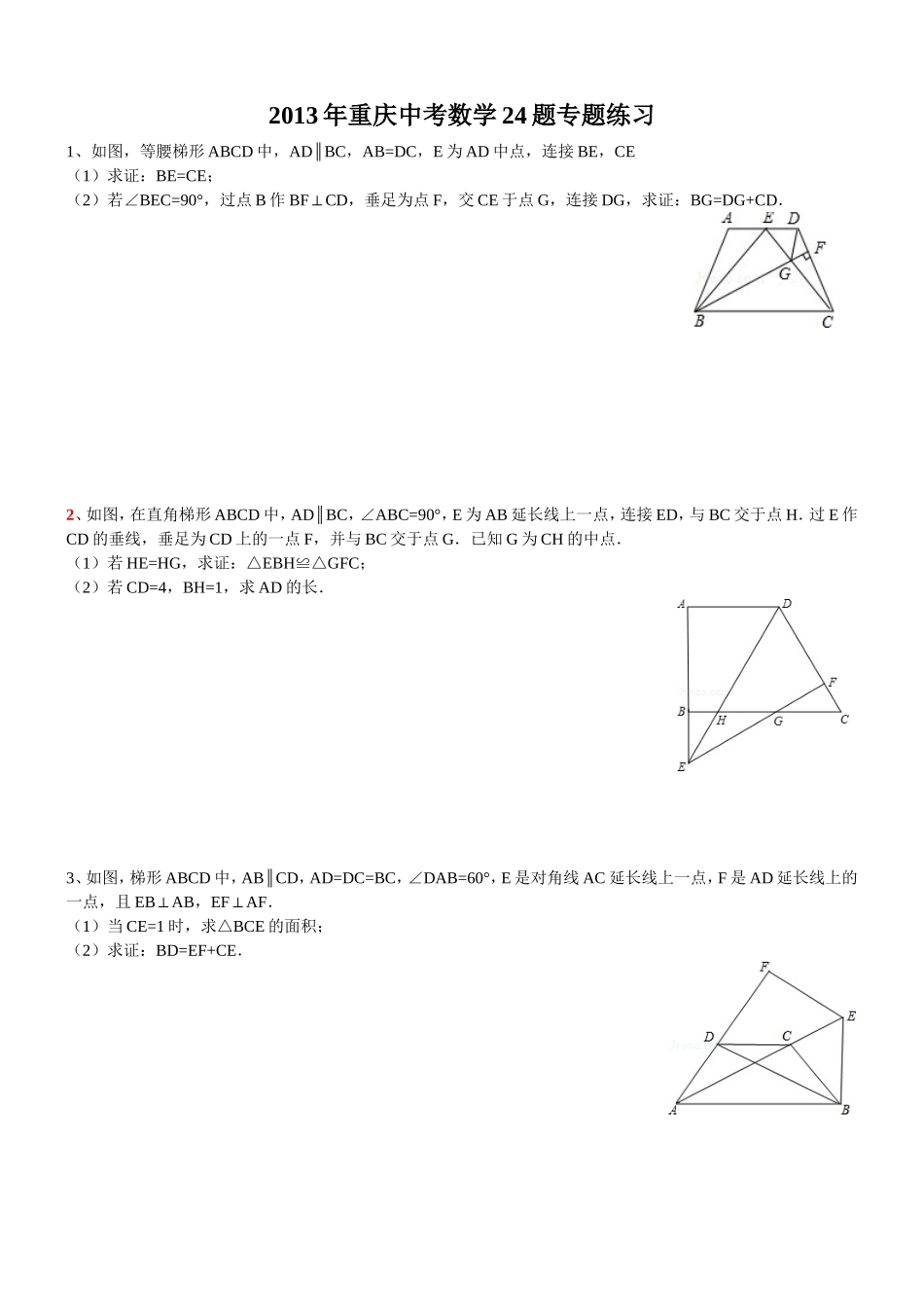
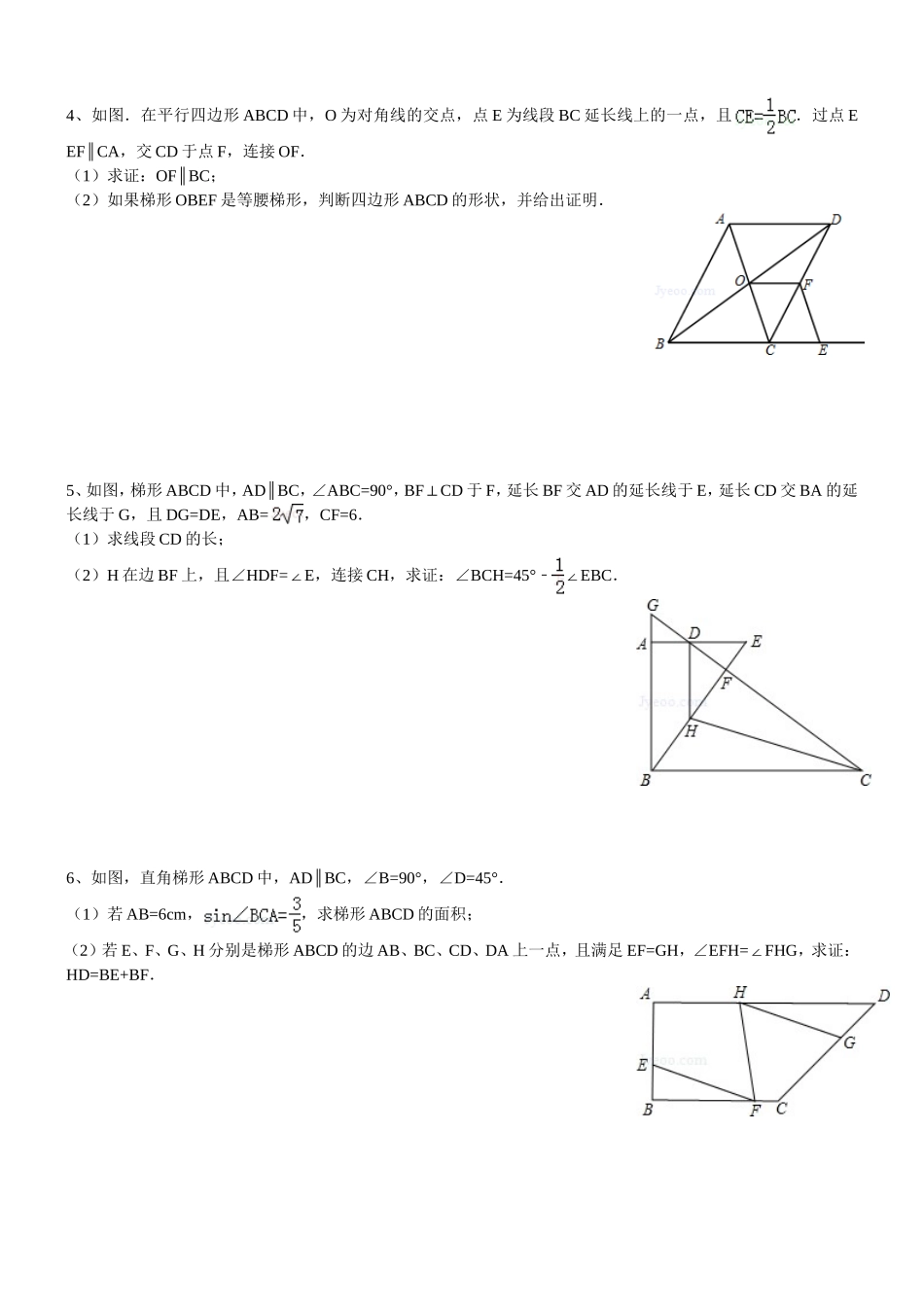
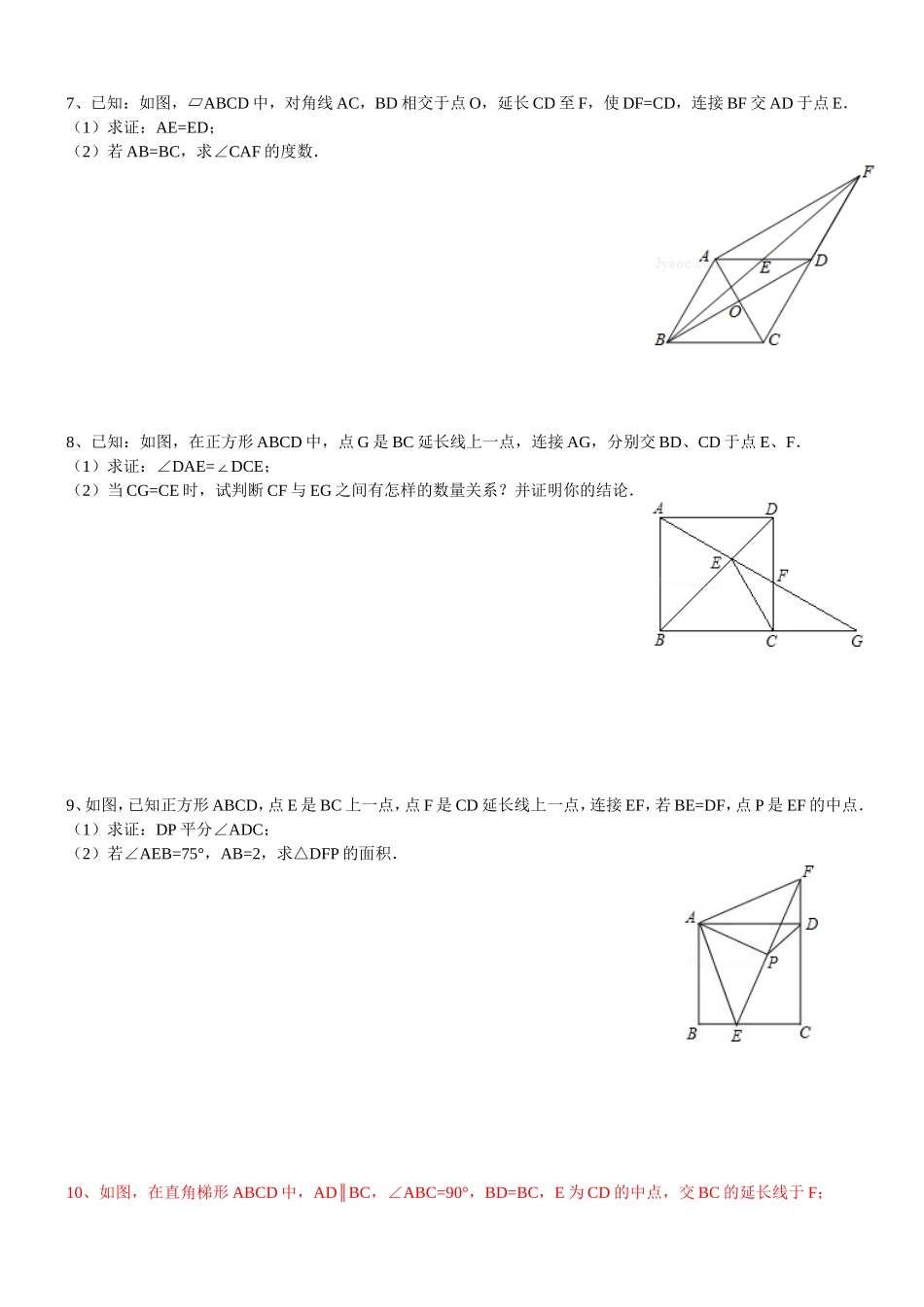
2013 年重庆中考数学 24 题专题练习1、如图,等腰梯形 ABCD 中,AD BC∥,AB=DC,E 为 AD 中点,连接 BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点 B 作 BFCD⊥,垂足为点 F,交 CE 于点 G,连接 DG,求证:BG=DG+CD.2、如图,在直角梯形 ABCD 中,AD BC∥,∠ABC=90°,E 为 AB 延长线上一点,连接 ED,与 BC 交于点 H.过 E 作CD 的垂线,垂足为 CD 上的一点 F,并与 BC 交于点 G.已知 G 为 CH 的中点.(1)若 HE=HG,求证:△EBHGFC≌△;(2)若 CD=4,BH=1,求 AD 的长.3、如图,梯形 ABCD 中,AB CD∥,AD=DC=BC,∠DAB=60°,E 是对角线 AC 延长线上一点,F 是 AD 延长线上的一点,且 EBAB⊥,EFAF⊥.(1)当 CE=1 时,求△BCE 的面积;(2)求证:BD=EF+CE.4、如图.在平行四边形 ABCD 中,O 为对角线的交点,点 E 为线段 BC 延长线上的一点,且.过点 E EF CA∥,交 CD 于点 F,连接 OF.(1)求证:OF BC∥;(2)如果梯形 OBEF 是等腰梯形,判断四边形 ABCD 的形状,并给出证明.5、如图,梯形 ABCD 中,AD BC∥,∠ABC=90°,BFCD⊥于 F,延长 BF 交 AD 的延长线于 E,延长 CD 交 BA 的延长线于 G,且 DG=DE,AB=,CF=6.(1)求线段 CD 的长;(2)H 在边 BF 上,且∠HDF=E∠ ,连接 CH,求证:∠BCH=45°﹣EBC∠.6、如图,直角梯形 ABCD 中,AD BC∥,∠B=90°,∠D=45°.(1)若 AB=6cm,,求梯形 ABCD 的面积;(2)若 E、F、G、H 分别是梯形 ABCD 的边 AB、BC、CD、DA 上一点,且满足 EF=GH,∠EFH=FHG∠,求证:HD=BE+BF.7、已知:如图,ABCD 中,对角线 AC,BD 相交于点 O,延长 CD 至 F,使 DF=CD,连接 BF 交 AD 于点 E.(1)求证:AE=ED;(2)若 AB=BC,求∠CAF 的度数.8、已知:如图,在正方形 ABCD 中,点 G 是 BC 延长线上一点,连接 AG,分别交 BD、CD 于点 E、F.(1)求证:∠DAE=DCE∠;(2)当 CG=CE 时,试判断 CF 与 EG 之间有怎样的数量关系?并证明你的结论.9、如图,已知正方形 ABCD,点 E 是 BC 上一点,点 F 是 CD 延长线上一点,连接 EF,若 BE=DF,点 P 是 EF 的中点.(1)求证:DP 平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP 的面积.10、如图,在直角梯形 ABCD 中,AD BC∥,∠ABC=90°,BD=BC,E 为 CD...