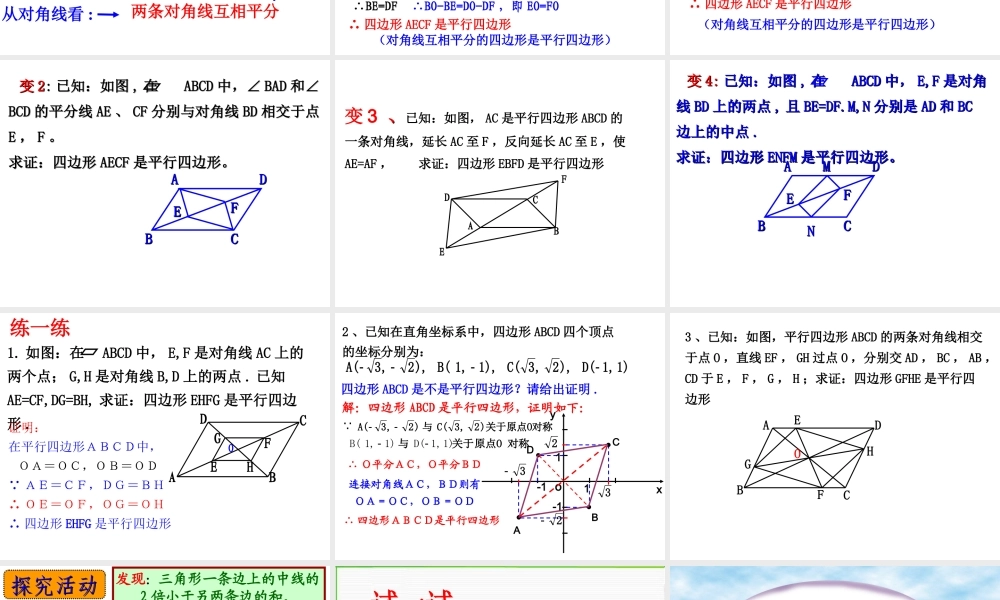
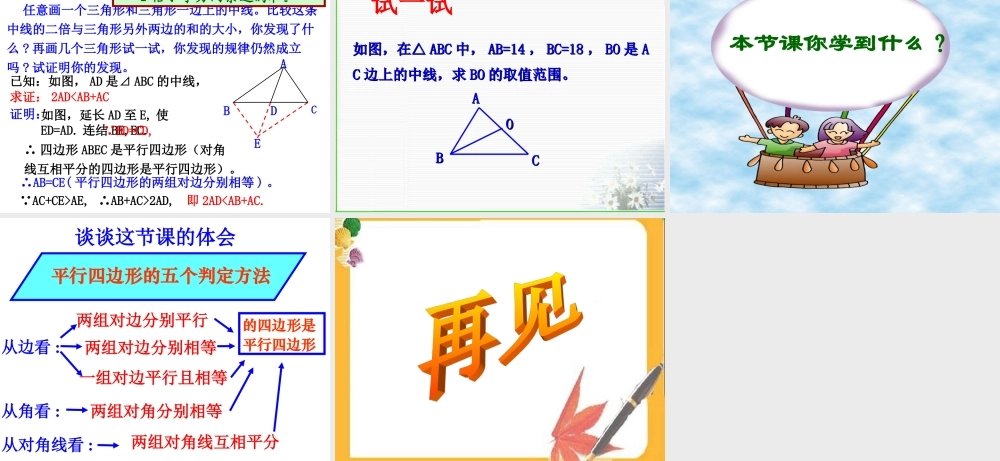
兰溪市第八中学 数学组平行四边形有哪些性质? Ⅰ. 边 :Ⅱ. 角 :Ⅲ. 对角线 :a. 平行四边形两组对边分别平行 .b. 平行四边形两组对边分别相等 .平行四边形两组对角分别相等 .平行四边形对角线互相平分 .DACB我们学过平行四边形有哪些判定方法? 从边看 : 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 问题:判定一个四边形是平行四边形是否还有其它的方法?ACOBD已知:在四边形 ABCD 中 , 对角线AC,BD交于点O, 且OA=OC,OB=OD ,求证:四边形 ABCD 是平行四边形证明:在△ AOD 与△ COB 中 AO=CO , DO=BO ,∠ AOD=∠COB∴△AOD≌△COB∴ AD=CB同理: AB=CD∴ 四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)定理 3 :两条对角线互相平分的四边形是平行四边形 .∴ 四边形ABCD是平行四边形平行四边形判定定理 3 :几何语言:如图 OA=OC , OB=OD(对角线互相平分的四边形是平行四边形)ABCDO从边看 : 平行四边形的四个判定方法两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 从对角线看 : 两条对角线互相平分 例例 11 、、已知:如图,已知:如图, EE ,, FF 是 是 ABCDABCD 的对角线的对角线BDBD 上的两点,且∠上的两点,且∠ BAE=∠DCFBAE=∠DCF求证:四边形求证:四边形 AECFAECF 是平行四边形。是平行四边形。AABBCCDDEEFFO证明 :连结 AC, 交 BD 于点 O AB∥CD在 ABCD 中, BO=DO ,AO=CO∴∠ABE=∠CDF又 ∠ BAE=∠CDF , AB=CD ∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF ,即 EO=FO∴ 四边形 AECF 是平行四边形(平行四边形的对角线互相平分)(平行四边形的定义)(对角线互相平分的四边形是平行四边形)变 1 、、已知:如图,已知:如图, EE ,, FF 是 是 ABCDABCD 的对角的对角线线 BDBD 上的两点,且 上的两点,且 BE=DF 求证:四边形求证:四边形 AECFAECF 是平行四边形。是平行四边形。AABBCCDDEEFFO证明 :连结 AC, 交 BD 于点 O在 ABCD 中, BO=DO ,AO=CO BO=DO BE=DF∴BO-BE=DO-DF ,即 EO=FO∴ 四边形 AECF 是平行四边形(平行四边形的对角线互相平分)(对角线互相平分的四边形是平行四边形) 变变 22:: 已知:如图已知:如图 ,, 在 在 ABCDABCD 中,∠中,∠ BADBAD 和∠...