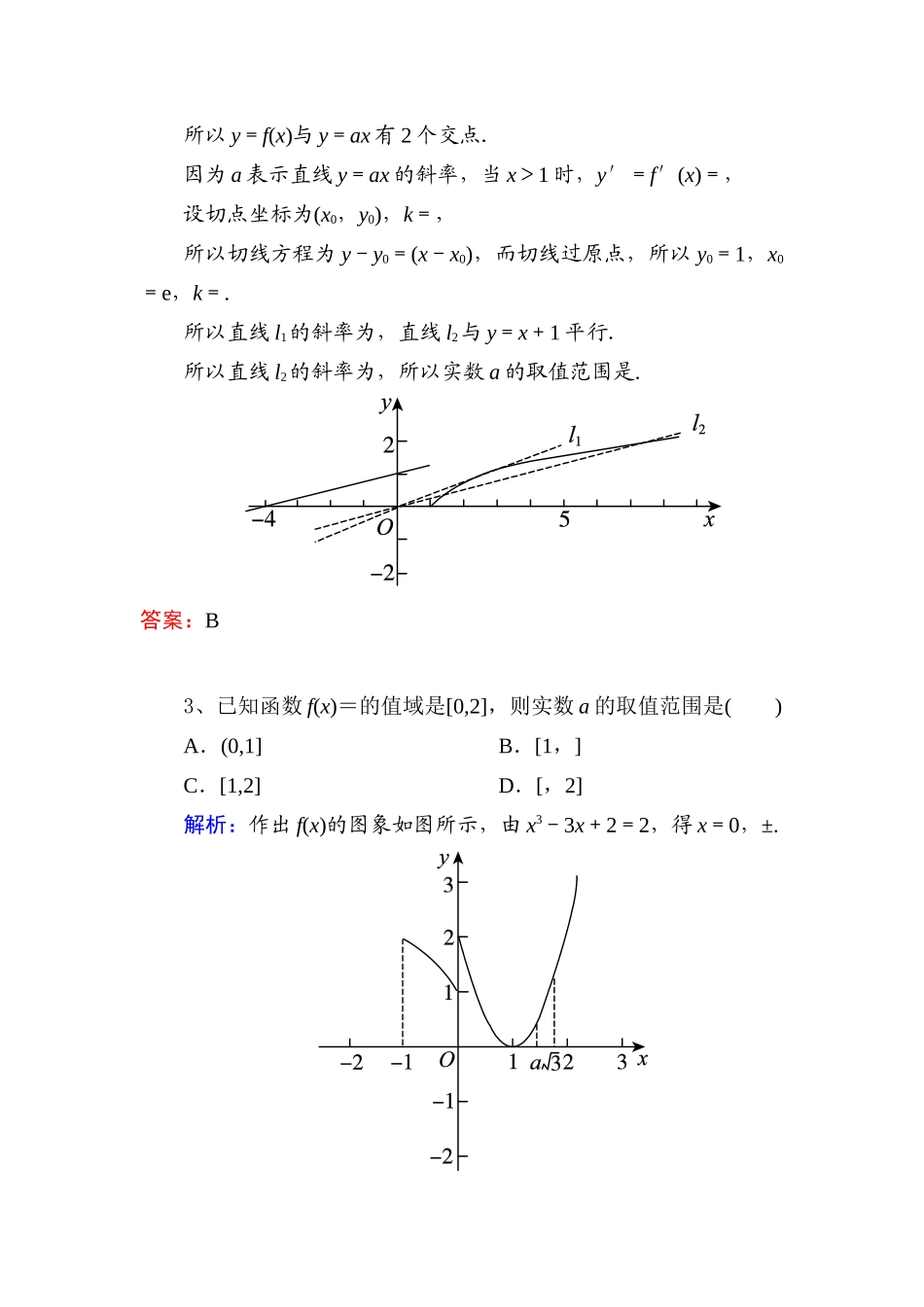
1、若函数f(x)满足f(x)+1=,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-2m有两个零点,则实数m的取值范围是()A.0<m≤B.0<m<C.<m≤1D.<m<1解析:g(x)=f(x)-mx-2m有两个零点,即曲线y=f(x),y=mx+2m有两个交点.令x∈(-1,0),则x+1∈(0,1),所以f(x+1)==x+1,f(x)=-1.在同一平面直角坐标系中,画出y=f(x),y=mx+2m的图象(如图所示),直线y=mx+2m过定点(-2,0),所以m满足0<m≤,即0<m≤,故选A.答案:A2、已知函数f(x)=则方程f(x)=ax恰有两个不同的实数根时,实数a的取值范围是(注:e为自然对数的底数)()A.B.C.D.解析:因为方程f(x)=ax恰有两个不同的实数根,所以y=f(x)与y=ax有2个交点.因为a表示直线y=ax的斜率,当x>1时,y′=f′(x)=,设切点坐标为(x0,y0),k=,所以切线方程为y-y0=(x-x0),而切线过原点,所以y0=1,x0=e,k=.所以直线l1的斜率为,直线l2与y=x+1平行.所以直线l2的斜率为,所以实数a的取值范围是.答案:B3、已知函数f(x)=的值域是[0,2],则实数a的取值范围是()A.(0,1]B.[1,]C.[1,2]D.[,2]解析:作出f(x)的图象如图所示,由x3-3x+2=2,得x=0,±.将f(x)=x3-3x+2求导得f′(x)=3x2-3,易得f(1)=0是f(x)的极小值.由图可知,要使得f(x)的值域是[0,2],需1≤a≤,故选B.答案:B4、已知函数f(x)=|x2-4x+3|.若关于x的方程f(x)-a=x至少有三个不相等的实数根,则实数a的取值范围为.解析:f(x)=作出图象如图所示.原方程变形为|x2-4x+3|=x+a.于是,设y=x+a,在同一坐标系下再作出y=x+a的图象.如图.则当直线y=x+a过点(1,0)时a=-1;当直线y=x+a与抛物线y=-x2+4x-3相切时,由⇒x2-3x+a+3=0.由Δ=9-4(3+a)=0,得a=-.由图象知当a∈时方程至少有三个不等实根.6、已知函数f(x)=若af(-a)>0,则实数a的取值范围是()A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)(1∪,+∞)D.(-∞,-1)(0∪,1)解析:当a>0时,a·f(-a)=a·log\f(1,2a>0,则0
0,则-1f(2),可得就必须有loga(2+1)>f(2)=-2,∴可得loga3>-2,∴3<,解得-0,∴00)与函数f(x)的图象恰好有3个不同的交点,则实数k的取值范围是()A.B.C.D.解析:画出函数f(x)=g(x)=k(x+1)(k>0)的图象,若直线y=kx+k(k>0)与函数y=f(x)的图象恰有三个不同的交点,结合图象可得:kPB≤k0时无零点;当a=0时有2个零点;当a<0时有4个零点.答案:②④