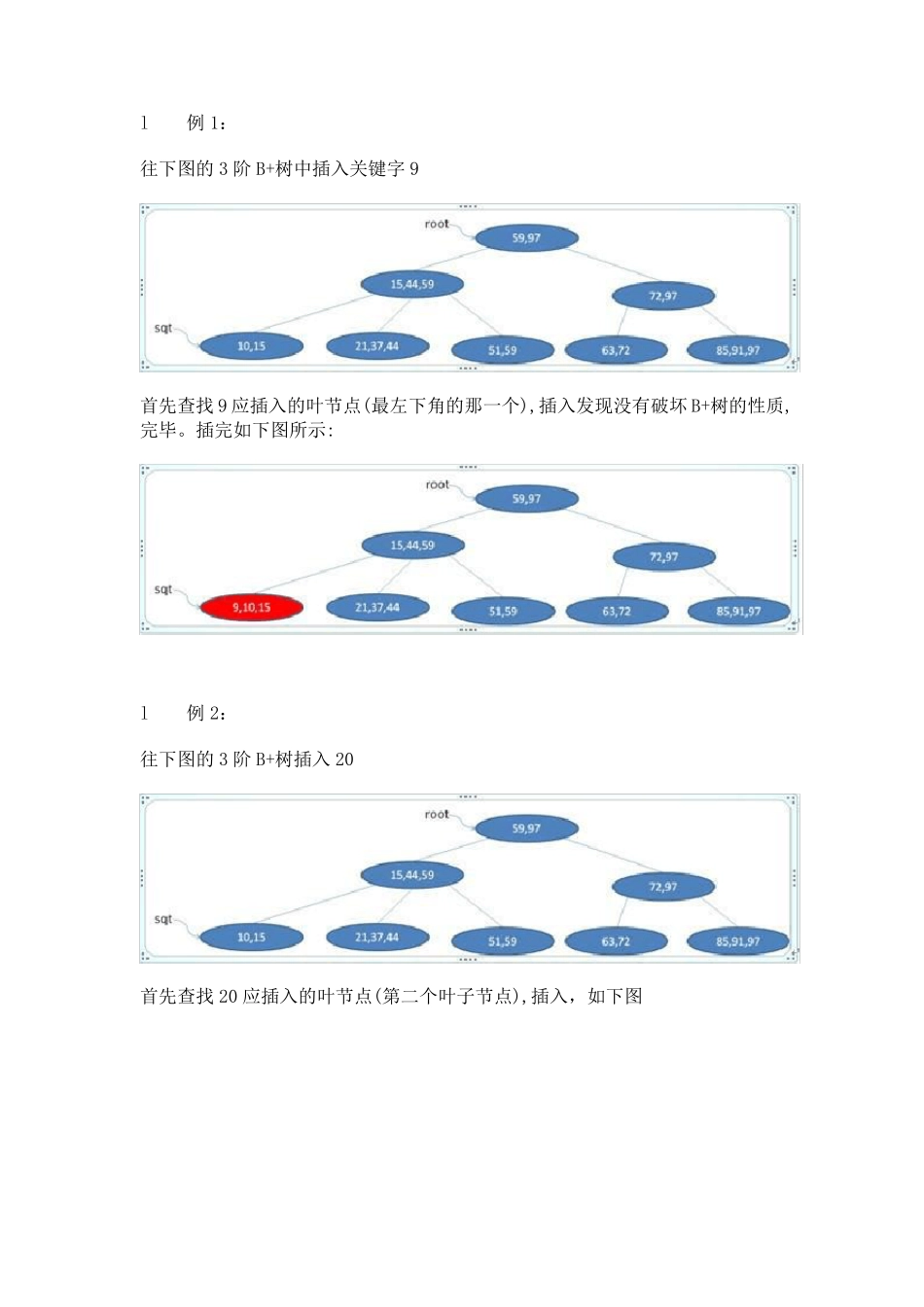
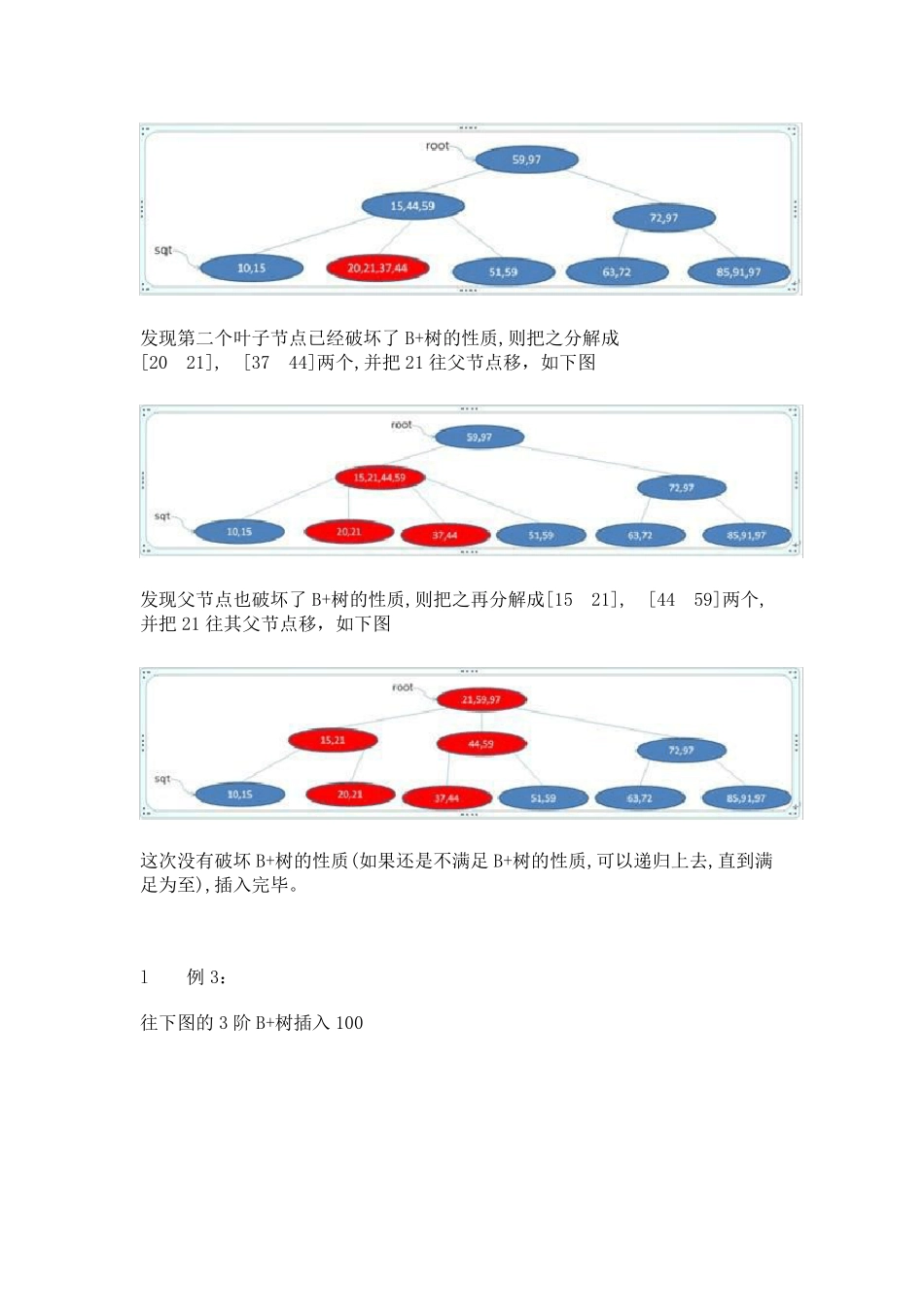
图解B+树的插入和删除(一看就懂) 一, M 阶B+树的定义(M 阶是指一个节点最多能拥有的孩子数,M>2): 图 1.1 3 阶 B+树 (1)根结点只有1 个,分支数量范围[2,m]。 (2)除根以外的非叶子结点,每个结点包含分支数范围[[m/2],m],其中[m/2]表示取大于m/2 的最小整数。 (3)所有非叶子节点的关键字数目等于它的分支数量。 (4) 所有叶子节点都在同一层,且关键字数目范围是[[m/2],m],其中[m/2]表示取大于m/2 的最小整数。 (5)所有非叶子节点的关键字可以看成是索引部分,这些索引等于其子树(根结点)中的最大(或最小)关键字。例如一个非叶子节点包含信息: (n,A0,K0, A1,K1,……,Kn,An),其中Ki 为关键字,Ai 为指向子树根结点的指针,n 表示关键字个数。即 Ai 所指子树中的关键字均小于或等于Ki,而Ai+1 所指的关键字均大于Ki(i=1,2,……,n)。 (6)叶子节点包含全部关键字的信息(非叶子节点只包含索引),且叶子结点中的所有关键字依照大小顺序链接(所以一个B+树通常有两个头指针,一个是指向根节点的root,另一个是指向最小关键字的sqt)。 二, 3 阶B+树的插入举例: l 例1: 往下图的3 阶B+树中插入关键字9 首先查找9 应插入的叶节点(最左下角的那一个),插入发现没有破坏B+树的性质,完毕。插完如下图所示: l 例2: 往下图的3 阶B+树插入20 首先查找20 应插入的叶节点(第二个叶子节点),插入,如下图 发现第二个叶子节点已经破坏了B+树的性质,则把之分解成[20 21], [37 44]两个,并把21 往父节点移,如下图 发现父节点也破坏了B+树的性质,则把之再分解成[15 21], [44 59]两个,并把21 往其父节点移,如下图 这次没有破坏B+树的性质(如果还是不满足B+树的性质,可以递归上去,直到满足为至),插入完毕。 l 例 3: 往下图的3 阶 B+树插入100 首先查找100 应插入的叶节点(最后一个节点), 插入,如下图 修改其所有父辈节点的键值为 100(只有插入比当前树的最大数大的数时要做此步),如下图 然后重复 Eg.2 的方法拆分节点,最后得 三, 3 阶 B+树的删除举例: l 例1: 删除下图3 阶B+树的关键字91 首先找到91 所在叶节点(最后一个节点),删除之,如下图 没有破坏 B+树的性质,删除完毕 l 例2: 删除下图3 阶B+树的关键字97 首先找到97 所在叶节点(最后一个节点),删除之,然后修改该节点的父辈的键字为 91(只有删除树中最大数时要做此步),如下图 l 例3: 删除下图3 阶...