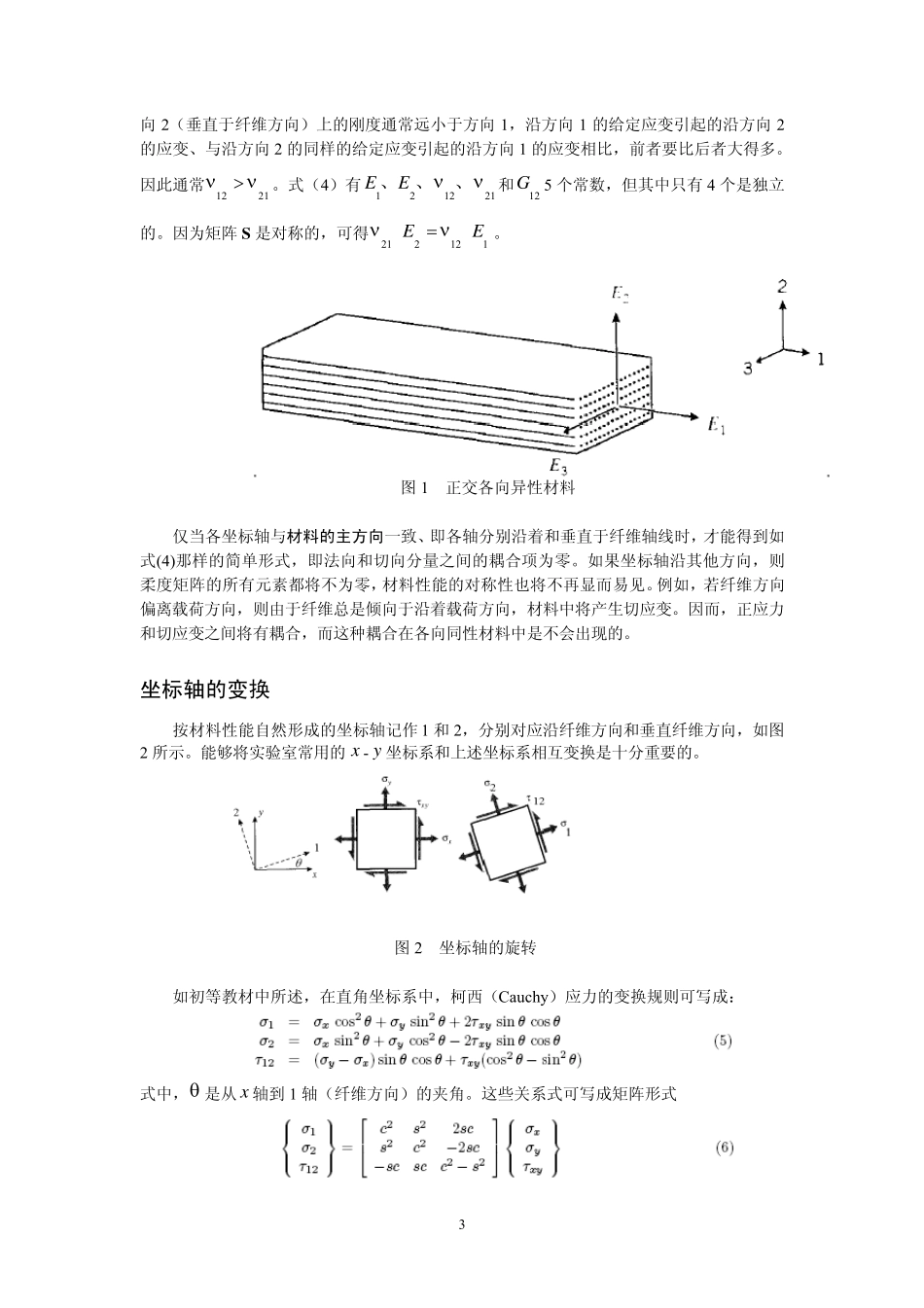
复合材料层合板 MA 02139,剑桥 麻省理工学院 材料科学与工程系 David Roylance 2000 年2 月10 日 引言 本模块旨在概略介绍纤维增强复合材料层合板的力学知识;并推导一种计算方法,以建立层合板的平面内应变和曲率与横截面上内力和内力偶之间的关系。虽然这只是纤维增强复合材料整个领域、甚至层合板理论的很小一部分,但却是所有的复合材料工程师都应掌握的重要技术。 在下文中,我们将回顾各向同性材料矩阵形式的本构关系,然后直截了当地推广到横观各向同性复合材料层合板。因为层合板中每一层的取向是任意的,我们随后将说明,如何将每个单层的弹性性能都变换到一个共用的方向上。最后,令单层的应力与其横截面上的内力和内力偶相对应,从而导出控制整块层合板内力和变形关系的矩阵。 层合板的力学计算最好由计算机来完成。本文简略介绍了几种算法,这些算法分别适用于 弹性层合板、呈 现 热 膨 胀 效 应的层合板和呈 现 粘 弹性响 应的层合板。 各向同性线弹性材料 如初 等 材料力学教 材( 参 见 罗 兰 奈 斯 ( Roylance) 所著 、1996 年出版 的教 材1) 中所述 ,在直角 坐 标 系中,由平面应力状 态 (0===yzxzzττσ) 导致 的应变为 由于 泊 松 效 应,在平面应力状 态 中还 有沿轴 方向的应变:z)(yxzσσνε+−=,此 应变分量 在下文中将忽 略不 计。在上述 关系式中,有三 个弹性常 量 : 杨 氏 模量 E 、泊 松 比 ν 和切 变模量。但对各向同性材料,只有两 个独 立的弹性常 量 ,例 如,G 可 从GE 和ν 得 到 上述 应力应变关系可 用矩阵记 号 写 成 1 参 见 本模块末 尾 所列 的参 考 资 料。 1 方括号内的量称为材料的柔度矩阵,记作S或。弄清楚矩阵中各项的物理意义十分重要。从矩阵乘法的规则可知,中第i 行第列的元素表示第个应力对第i 个应变的影响。例如,在位置1,2 上的元素表示方向的应力对jiSjiSjjyx 方向应变的影响:将E1乘以yσ 即得由yσ引起的方向的应变,再将此值乘以yν−,得到yσ 在x 方向引起的泊松应变。而矩阵中的零元素则表示法向分量和切向分量之间无耦合,即互不影响。 如果我们想用应变来表示应力,则式(1)可改写为: 式中,已用G)1(2ν+E代替。该式可进一步简写为: 式中, 是刚度矩阵。注意:柔度矩阵S中1,1 元素的倒数即为杨氏模量,但是刚度矩阵中的1,11SD−=D元素...