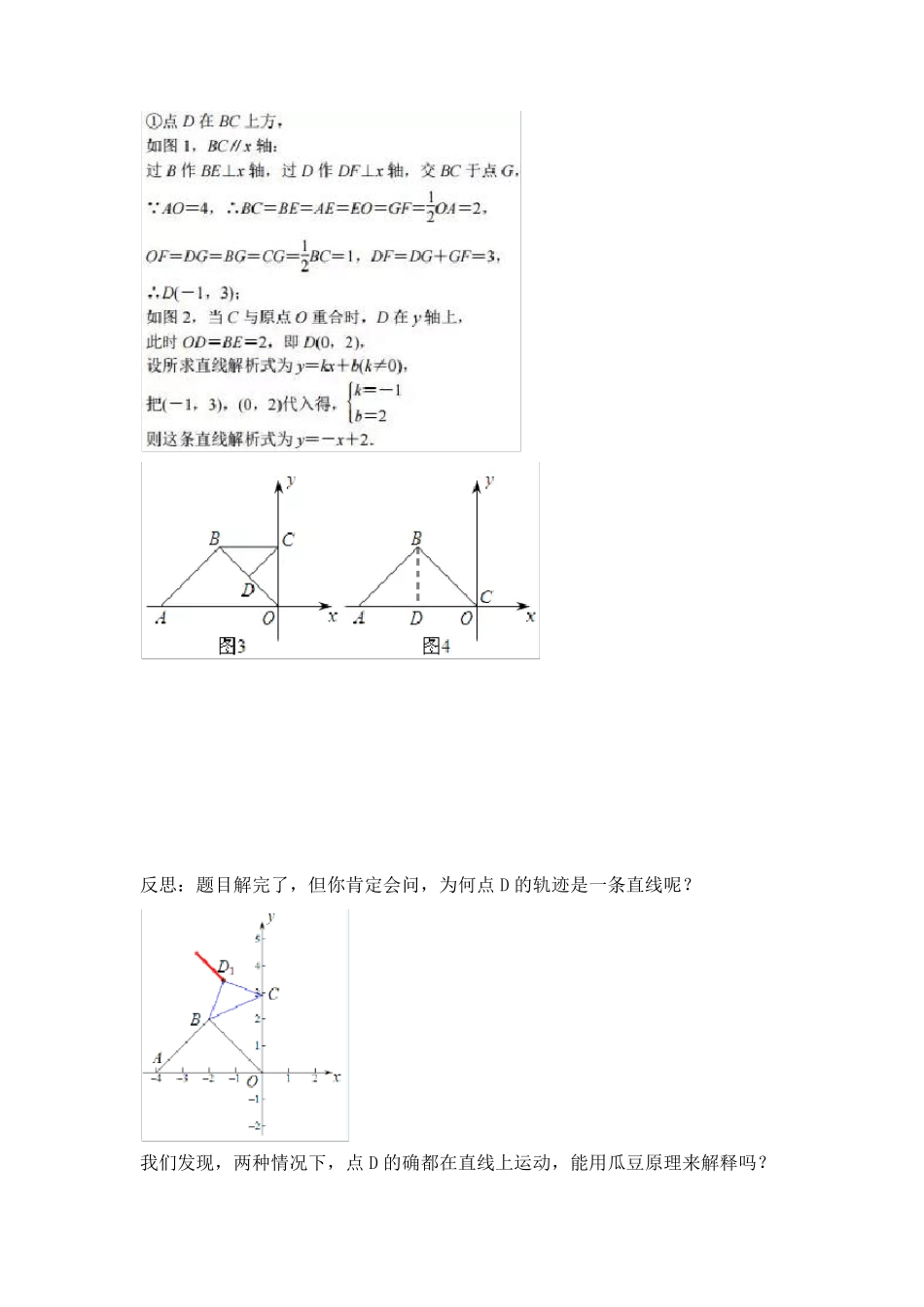
中考数学压轴题必考 破解瓜豆原理的三种必考题型 一.轨迹解析式 例1:如图,△ABO 为等腰直角三角形,A(-4,0),直角顶点 B 在第二象限,点 C 在 y 轴上移动,以 BC 为斜边作等腰直角△BCD,我们发现直角顶点 D 点随着 C 点的移动也在一条直线上移动,这条直线的函数解析式是_________ 分析:我们先来看看当时的解法.显然,由于题目已经明确给出点 D 的轨迹是一条直线,那么,可以采用特殊值法来考虑,选取两个特殊位置的点 C,确定相应的点 D 的坐标,两点确定一条直线即可. 当然,本题要分两种情况,点 D 在 BC 上方,和点 D 在 BC 下方. 解答: 反思:题目解完了,但你肯定会问,为何点D 的轨迹是一条直线呢? 我们发现,两种情况下,点D 的确都在直线上运动,能用瓜豆原理来解释吗? 何为瓜豆原理?下面就具体来解释下瓜豆原理的由来: 由此可见,在旋转放缩过程中, 从动点和主动点的轨迹是一致的! 即所谓“种瓜得瓜,种豆得豆”也! 而本题若用一般方法求解,也不难,构造一线三直角全等可破. 解答: 二.求经过的路径长 例2:如图,正方形ABCD 的边长为2,动点E 从点A 出发,沿边AB 向终点B运动,以DE 为边作正方形DEFG(点D、E、F、G 按顺时针方向排列).求在点E的整个运动过程中,点F 经过的路径长. 分析: 解答: 当点E 与 A 点重合时,点F 在点B 处: 当点E 与 B 点重合时,点F 的位置如下图所示, 点F 运动的路径为BF; 三.求最值问题 例3:如图,在直角坐标系中,已知点A(4,0),点B 为y 轴正半轴上一动点,连接AB,以AB 为一边向下作等边△ABC,连接OC,则OC 的最小值_________. 分析:点B 为主动点,点C 为从动点,根据瓜豆原理,BA 绕点A 逆时针旋转60°到 CA,主动点B 的轨迹是 y 轴的正半轴,则从动点C 的运动轨迹为y 轴正半轴绕点A 逆时针旋转60°后的射线,我们可以用特殊位置来考虑.当 OC⊥点C 轨迹所在射线时,OC 最短. 当然,我们也可以构造手拉手模型,将 OC 边转化,详细过程请见方法 2. 解答: 方法一: 方 法 二 :