凸轮的matlab绘制VIP免费

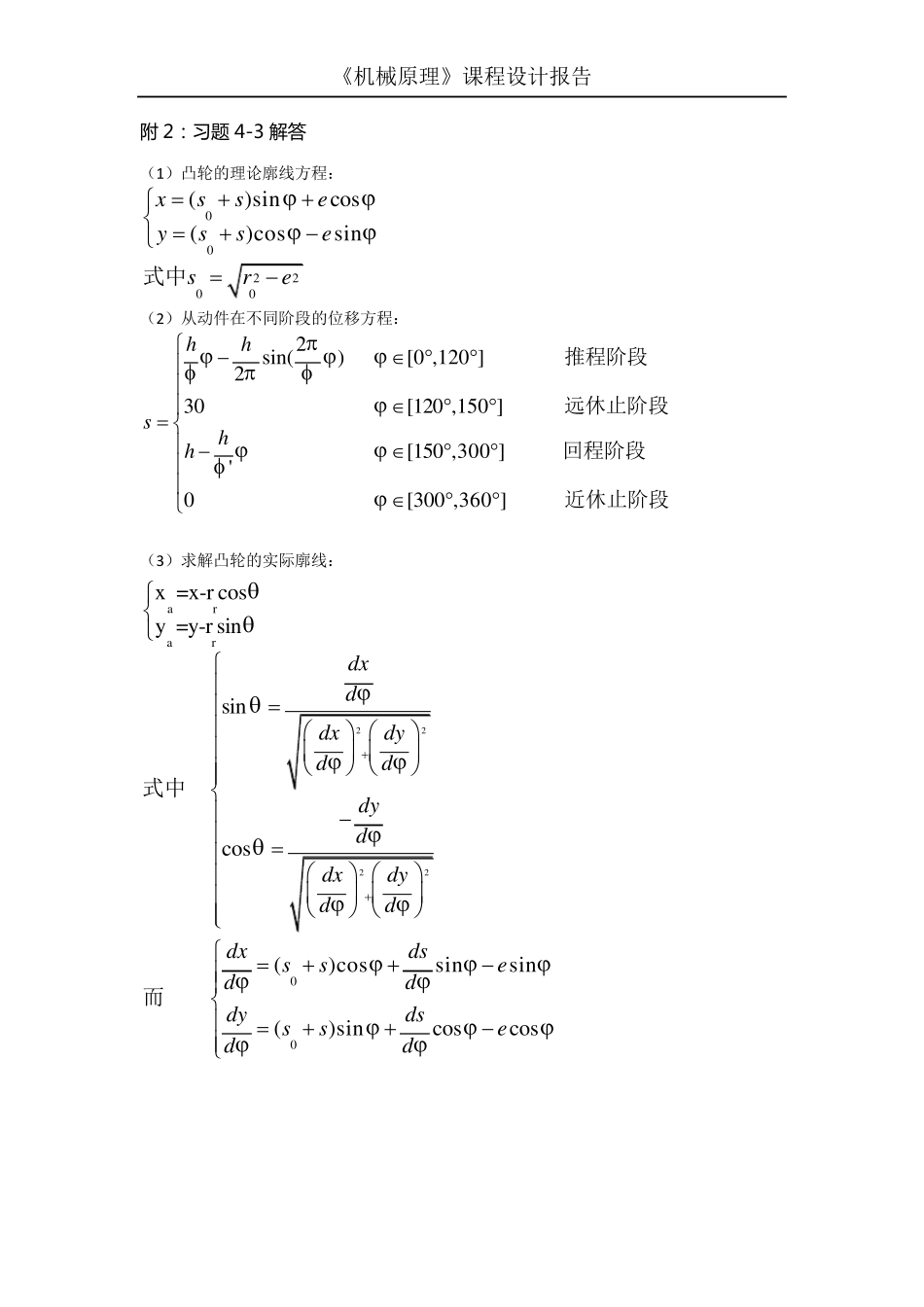
《机械原理》课程设计报告 附 2： 习题 4-3 解答 （1 ）凸轮的理论廓线方程： 002200()sincos()cossinxsseyssesre式中 （2 ）从动件在不同阶段的位移方程： 2sin()[0 ,120 ]230[120 ,150 ][150 ,300 ]'0[300 ,360 ]hhshh  推程阶段远休止阶段回程阶段近休止阶段 （3 ）求解凸轮的实际廓线： 2222arar00x =x-r cosy =y-r sinsincos()cossinsin()sincoscosdxddxdydddyddxdydddxdsssedddydsssedd      式中而 《机械原理》课程设计报告 同样，由于位移 s 与从动件所处的运动阶段有关，所以有： 2cos()[0 ,120 ]0[120 ,150 ]s[150 ,300 ]'0[300 ,360 ]hhdhd  推程阶段远休止阶段回程阶段近休止阶段 （4）代入已知条件，并用 Matlab 语言编程求解，编程代码如下： disp ' ******** 偏置直动滚子从动件盘形凸轮设计 ********' disp '已知条件:' disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边' disp ' 从动件在推程作摆线运动规律运动,在回程作等速运动规律运动' ro = 50;rr = 10;e = 12;h = 30;ft = 120;fs = 30;fh = 150; fprintf (1,' 基圆半径 ro = %3.4f mm \n',ro) fprintf (1,' 滚子半径 rr = %3.4f mm \n',rr) fprintf (1,' 推杆偏距 e = %3.4f mm \n',e) fprintf (1,' 推程行程 h = %3.4f mm \n',h) fprintf (1,' 推程运动角 ft = %3.4f 度 \n',ft) fprintf (1,' 远休止角 fs = %3.4f 度 \n',fs) fprintf (1,' 回程运动角 fh = %3.4f 度 \n',fh) hd = pi / 180;du = 180 / pi; so = sqrt( ro^2 - e^2 ); d1 = ft + fs;d2 = ft + fs + fh; disp ' ' disp '计算过程和输出结果:' disp ' 1-1 推程(摆线运动规律运动)' s = zeros(ft);ds = zeros(ft);d2s = zeros(ft); for f = 1 : ft s(f) = h * f / ft - h * sin(2 * pi * f / ft) / (2 * pi);s = s(f);...