共线向量和共面向量VIP免费

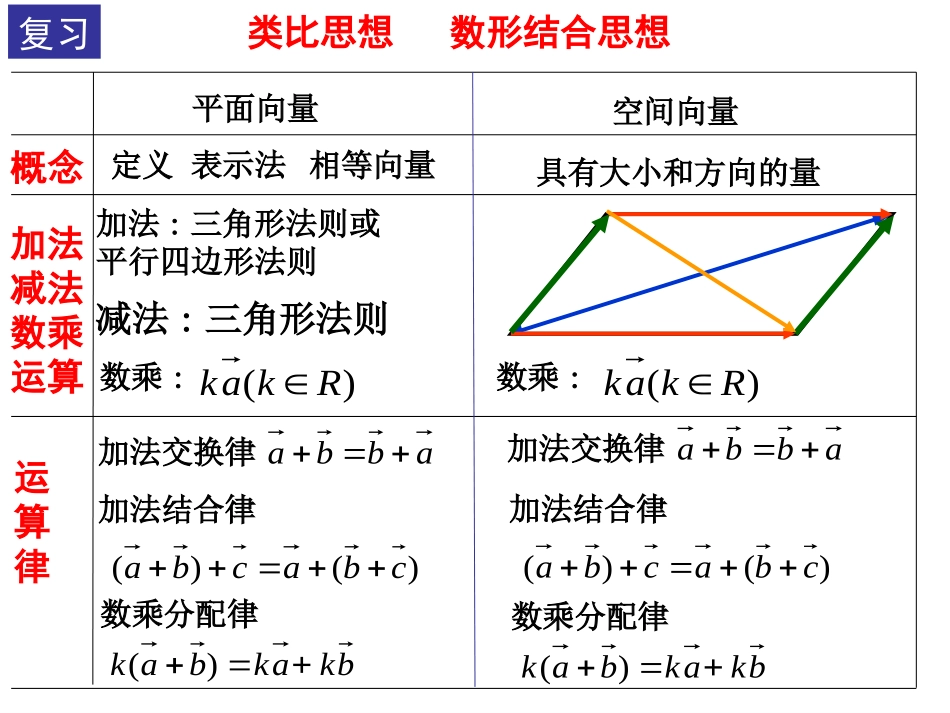
共线向量与共面共线向量与共面向量向量共线向量与共面共线向量与共面向量向量aÒƶ¯C'D'B'A'CABD湖南省临湘市一中李君英平面向量概念加法减法数乘运算运算律定义表示法相等向量减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量数乘:bkakbak＋)()()(cbacbaabba加法交换律加法结合律数乘分配律复习abba加法交换律bkakbak＋)(数乘分配律)()(cbacba加法结合律类比思想数形结合思想数乘:)(Rkak)(Rkak平面向量共线定理：方向相同或者相反的非零向量叫做平行向量．平面共线向量的定义：由于任何一组平行向量都可以平移到同一条直线上，所以平行向量也叫做共线向量．bca向量与非零向量共线的充要条件是有且只有一个实数使得abba=,要注意其中对向量的非零要求．a规定:与任一向量共线.0一、空间共线向量1.共线向量:与平面向量一样,如果表示空间向量的有向线段所在直线互相平行或重合,这些向量叫做共线向量(或平行向量).bca平行于,记作∥abab规定零向量与任意向量共线.注意:2.共线向量定理:符号语言:Rbab//abb,a0使是存在实数的充要条件对空间任意两个向量)0(,bbaba//,ba2.共线向量定理:的充要条件对空间任意两个向量)0(,bbaba//,是存在实数ba使bca注意:2.定理的应用②充分性是空间向量共线的判定定理1.该定理中的不能忽视,否则不存在或不唯一0b①必要性是共线向量的性质定理当用向量共线判断直线平行时,要注意向量平行与直线平行的区别3.在中,对于确定的和,表示空间与平行且长度为的所有向量abaaaab推论：如果为经过已知点A且平行于已知非零向量的直线，那么对任一点O，点P在直线上的充要条件是存在实数满足等式：alltOPOAta（注意：点P在上的位置与存在一一对应关系）ltOABPa12�OPOAOB当时，点P是线段AB的中点，此时有：21t)yx(OByOAxOP1P、A、B三点共线线段AB的中点公式ltOBOAtOP)1(或空间直线的向量参数表示式直线l的方向向量tOBOA)t(OP11.下列说法正确的是()A.在平面内共线的向量在空间不一定共线B.在空间共线的向量在平面内不一定共线C.在平面内共线的向量在空间一定不共线D.在空间共线的向量在平面内一定共线练习2.对于空间任意一点O，下列命题正确的是：()A.若，则P、A、B共线B.若，则P是AB的中点C.若，则P、A、B不共线D.若，则P、A、B共线DA二.共面向量1.向量与平面平行的定义OAaa如果直线OA平行于平面2.共面向量平行于同一平面的向量,叫做共面向量⑵空间中任意三个向量一定是共面向量吗?思考:⑴共面向量一定是在同一平面吗?已知平面与向量,作aOAa或在内a,就说向量平行于平面a//a记作CABD3.空间中三个向量共面的条件已知向量p,b,a⑴若b//a⑵若不共线,空间任一向量在什么条件下与它们共面?b,apabp,则这三个向量一定共面bapMBAP'A反之,若存在实数对(x,y)使ybxapabp若与共面,根据平面向量基本定理,一定存在实数对x,y使b,apybxapxa'MA作ybP'ApybxaMP则于是向量∥平面MABp即与共面pb,a平面向量的基本定理如果、是同一平面内的两个不共线的向量，那么对于这一平面内的任一向量，有且只有一对实数、使1e2ea12a11e22e共面向量定理如果两个向量，不共线，则向量与向量，共面的充要条件是存在实数对x，y，使abpabybxapMBAP'AabpabOMBAP'A或对空间任一点O,有�MPxMAyMB�OPOMxMAyMB平面MAB的向量表达式。推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使说明:此推论是证明点在平面内(点共面)的依据..,,,)1(,,,.1是否共面的四点其中向量关系式试问满足和不共线的三点对空间任一点例CBAPzyxOCzOByOAxOPCBAOABCPO注：此结论与共面向量的推论只是形式不同，实质是一样的，都可用来证明四点共面。例２.如图：PA⊥平面ABCD,ABCD是矩形,M、N分别是AB、PC中点。求证：MN//平面PADBCADPMNEFPADMNAFMNAFAPADENMEMN面////2121ABCDOEFGH.//)2(.,,,)1(:,,,,,.3ACEGHGFEODkOHOCkOGOBkOFOAkOEOACABCD平面平面共面四...