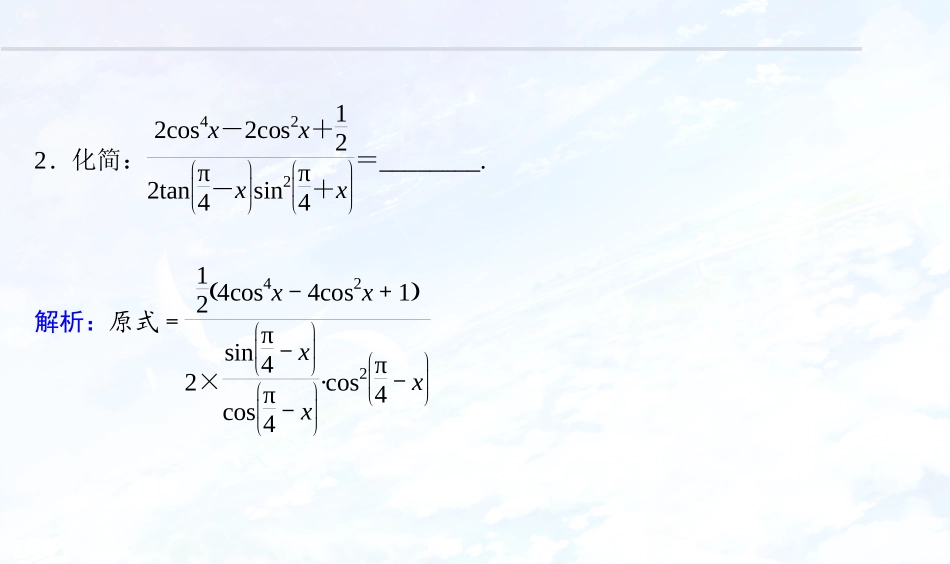简单的三角恒等变换VIP免费

简单的三角恒等变换题型一三角函数式的化简1．化简：sin2α－2cos2αsinα－π4＝________.解析：原式＝2sinαcosα－2cos2α22sinα－cosα＝22cosα.答案：22cosα2．化简：2cos4x－2cos2x＋122tanπ4－xsin2π4＋x＝________.解析：原式＝124cos4x－4cos2x＋12×sinπ4－xcosπ4－x·cos2π4－x＝2cos2x－124sinπ4－xcosπ4－x＝cos22x2sinπ2－2x＝cos22x2cos2x＝12cos2x.答案：12cos2x3．化简：sin2α＋βsinα－2cos(α＋β)．解：原式＝sin2α＋β－2sinαcosα＋βsinα＝sin[α＋α＋β]－2sinαcosα＋βsinα＝sinαcosα＋β＋cosαsinα＋β－2sinαcosα＋βsinα＝cosαsinα＋β－sinαcosα＋βsinα＝sin[α＋β－α]sinα＝sinβsinα.【思维升华】(1)三角函数式的化简要遵循“三看”原则一看角，二看名，三看式子结构与特征．(2)三角函数式的化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等)，寻找式子和三角函数公式之间的共同点．题型二三角函数的求值命题点1给角求值与给值求值例1(1)[2sin50°＋sin10°(1＋3tan10°)]·2sin280°＝________.解析：原式＝2sin50°＋sin10°·cos10°＋3sin10°cos10°·2sin80°＝2sin50°＋2sin10°·12cos10°＋32sin10°cos10°·2cos10°＝22[sin50°·cos10°＋sin10°·cos(60°－10°)]＝22sin(50°＋10°)＝22×32＝6.答案：6(2)已知cosθ＋π4＝1010，θ∈0，π2，则sin2θ－π3＝________.解析：由题意可得cos2θ＋π4＝1＋cos2θ＋π22＝110，cos2θ＋π2＝－sin2θ＝－45，即sin2θ＝45.因为cosθ＋π4＝1010>0，θ∈0，π2，所以0<θ<π4，2θ∈0，π2，根据同角三角函数基本关系式，可得cos2θ＝35，由两角差的正弦公式，可得sin2θ－π3＝sin2θcosπ3－cos2θsinπ3＝45×12－35×32＝4－3310.答案：4－3310命题点2给值求角例2(1)设α，β为钝角，且sinα＝55，cosβ＝－31010，则α＋β的值为()A.3π4B．5π4C.7π4D．5π4或7π4解析： α，β为钝角，sinα＝55，cosβ＝－31010，∴cosα＝－255，sinβ＝1010，∴cos(α＋β)＝cosαcosβ－sinαsinβ＝22>0.又α＋β∈(π，2π)，∴α＋β∈3π2，2π，∴α＋β＝7π4.答案：C(2)已知α，β∈(0，π)，且tan(α－β)＝12，tanβ＝－17，则2α－β的值为________．解析： tanα＝tan[(α－β)＋β]＝tanα－β＋tanβ1－tanα－βtanβ＝12－171＋12×17＝13>0，∴0<α<π4.又 tan2α＝2tanα1－tan2α＝2×131－132＝34>0，∴0<2α<π2，∴tan(2α－β)＝tan2α－tanβ1＋tan2αtanβ＝34＋171－34×17＝1. tanβ＝－17<0，∴π2<β<π，－π<2α－β<0，∴2α－β＝－3π4.答案：－3π4【思维升华】(1)给角求值与给值求值问题的关键在“变角”，通过角之间的联系寻找转化方法．(2)给值求角问题：先求角的某一三角函数值，再求角的范围确定角．跟踪训练1(1)已知α∈0，π2，且2sin2α－sinα·cosα－3cos2α＝0，则sinα＋π4sin2α＋cos2α＋1＝________.解析： α∈0，π2，且2sin2α－sinα·cosα－3cos2α＝0，则(2sinα－3cosα)·(sinα＋cosα)＝0，又 α∈0，π2，sinα＋cosα>0，∴2sinα＝3cosα，又sin2α＋cos2α＝1，∴cosα＝213，sinα＝313，∴sinα＋π4sin2α＋cos2α＋1＝22sinα＋cosαsinα＋cosα2＋cos2α－sin2α＝24cosα＝268.答案：268(2)已知sinα＝55，sin(α－β)＝－1010，α，β均为锐角，则β＝________.解析：因为α，β均为锐角，所以－π2<α－β<π2.又sin(α－β)＝－1010，所以cos(α－β)＝31010.又sinα＝55，所以cosα＝255，所以sin...