四柱坐标系和球坐标系简介VIP免费

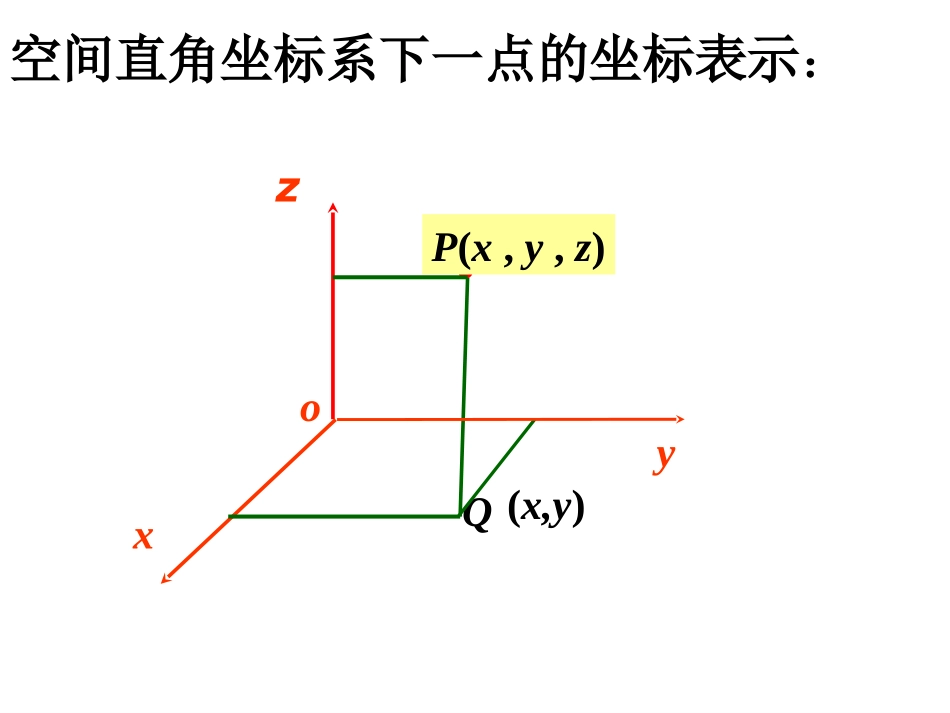
Q(x,y)xyozP空间直角坐标系下一点的坐标表示：P(x,y,z)1.1.柱坐标系柱坐标系思考：在一个圆形体育场内，如何确定看台上某个座位的位置？探究（一）：柱坐标系思考1：有一个圆形体育场，自正东方向起，按逆时针方向等分为十二个扇形区域，顺次记为一区，二区……十二区，那么每个座位票是如何设定的？第几区，第几排，第几座.思考2：设体育场第一排与体育场中心O的距离为300m，前后相邻两排的间距都为1m，每层看台的高度为0.6m，那么第九区第三排正中的位置A与体育场中心O的水平距离为多少m？从正东方向到位置A的水平旋转角是多少？位置A距地面的高度为多少m？302m，，1.8m1712思考3：根据坐标思想，可以用数组(302，，1.8)表示点A的准确位置，那么这个空间坐标系是如何建立的？1712xOz在水平面内建立极坐标系Ox，过极点O作水平面的垂线Oz.柱坐标系建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点，它在Oxy平面上的射影为Q，Q点的极坐标为(ρ,θ)，则P的位置可用有序数组(ρ,θ,z)表示，(ρ,θ,z)叫做点P的柱坐标.QθP(x,y,z)P(ρ,θ,z)(ρ,θ)xyzo柱坐标与空间直角坐标的互化x=ρcosθy=ρsinθz=z(1)柱坐标转化为直角坐标柱坐标与空间直角坐标的互化(2)直角坐标转化为柱坐标222tan(0)xyyxxzz1.设P点的柱坐标为，求它的直角坐标.2.设M点的直角坐标为求它的柱坐标.练习(1,3,3)(2,,7)6(3,1,7)4(2,,3)3思考：点P的柱坐标为(ρ,θ,z)，(1)当ρ为常数时，点P的轨迹是____(2)当θ为常数时，点P的轨迹是___(3)当z为常数时，点P的轨迹是_____圆柱面半平面平面θxyzoP(ρ,θ,z)(ρ,θ)Q小结小结1.柱坐标系学习目标：(1)理解柱坐标三个分量的几何意义；(2)掌握柱坐标与空间直角坐标的互化.2.柱坐标与空间直角坐标的互化cossinxyzz(1)柱坐标转化为直角坐标(2)直角坐标转化为柱坐标222tanxyyxzz2.2.球坐标系球坐标系思考：某市的经纬度：北纬42°，东经119°.地球的纬度地球的纬度与经度：球坐标系建立空间直角坐标系Oxyz.设P(x,y,z)是空间任意一点，记|OP|=r,OP与Oz轴正向所夹的角为.点P在Oxy平面上的射影为Q，Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.则P的位置可用有序数组(r,,)表示，(r,,)叫做点P的球坐标.球坐标系θxyzoQP(r,,)Pr0r020P(r,,)将球坐标转化为直角坐标：sincossinsincosxryrzrxθyoQP(r,,)rz0r0021.设Q点的球坐标为，求它的直角坐标.练习33(2,,)44(1,1,2)2.设M点的直角坐标为，那么它的球坐标是练习(1,1,2).(2,,)44A5.(2,,)44B5.(2,,)44C3.(2,,)44D思考：点P的球坐标为(r,,)，(1)当r为常数时，点P的轨迹是____(2)当为常数时，点P的轨迹是____(3)当为常数时，点P的轨迹是___球面圆锥面或平面半平面θxyzoQP(r,,)r小结小结1.球坐标系学习目标：(1)理解球坐标三个分量的几何意义；(2)能够将球坐标转化为直角坐标.2.将球坐标转化为直角坐标：sincossinsincosxryrzr