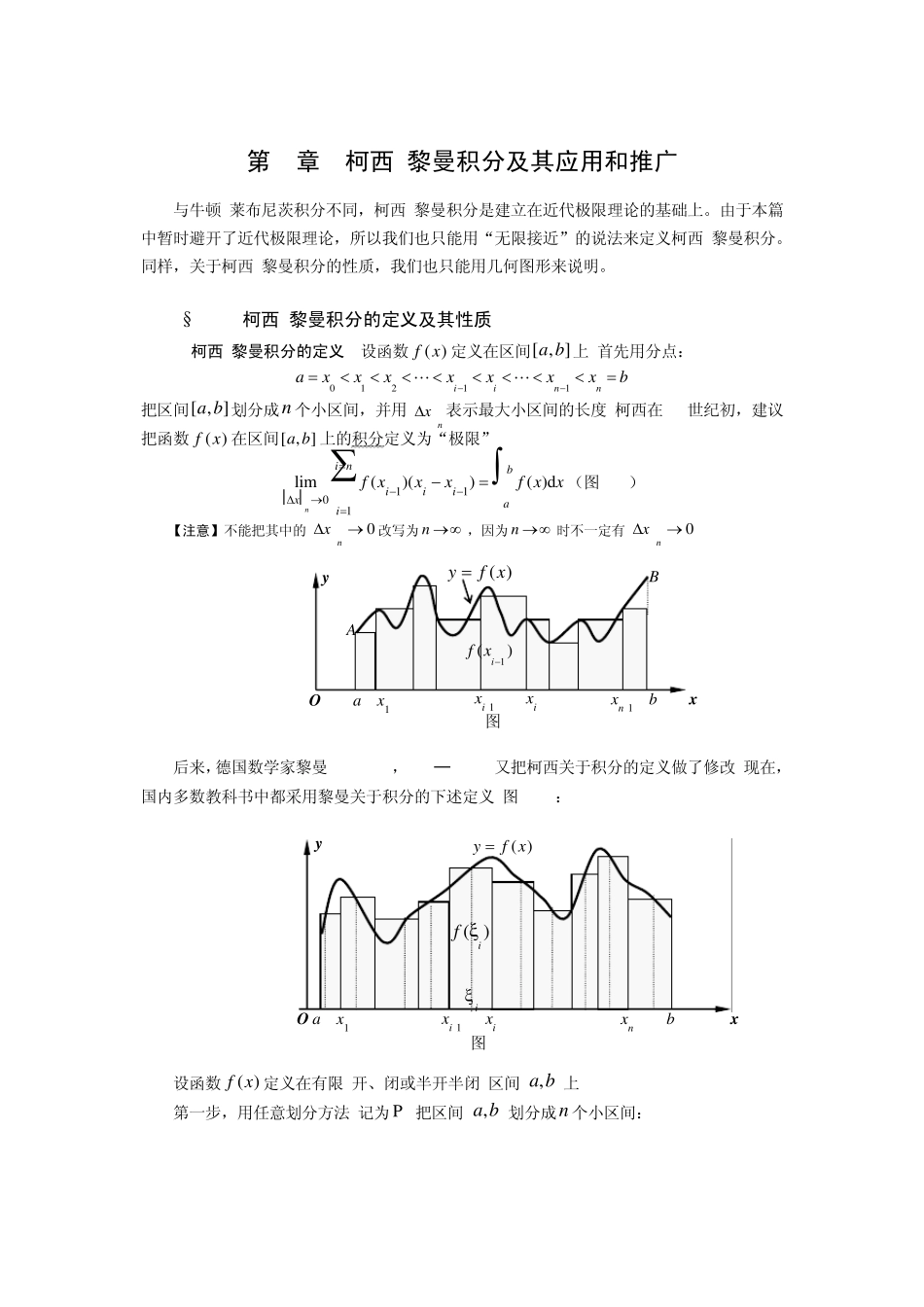
第4章 柯西-黎曼积分及其应用和推广 与牛顿-莱布尼茨积分不同,柯西-黎曼积分是建立在近代极限理论的基础上。由于本篇中暂时避开了近代极限理论,所以我们也只能用“无限接近”的说法来定义柯西-黎曼积分。同样,关于柯西-黎曼积分的性质,我们也只能用几何图形来说明。 §4-1 柯西-黎曼积分的定义及其性质 1.柯西-黎曼积分的定义 设函数)(xf定义在区间[ , ]a b 上.首先用分点: 01211iinnaxxxxxxxb 把区间[ , ]a b 划分成n 个小区间,并用nx表示最大小区间的长度.柯西在19世纪初,建议把函数)(xf在区间],[ba上的积分定义为“极限” 1101lim()()( )dni nbiiixaif xxxf xx(图 4-1) 【注意】不能把其中的0nx改写为 n ,因为 n 时不一定有0nx. 后来,德国数学家黎曼(Riemann,1826─1866 )又把柯西关于积分的定义做了修改.现在,国内多数教科书中都采用黎曼关于积分的下述定义(图 4-2): 设函数)(xf定义在有限(开、闭或半开半闭)区间ba,上. 第一步,用任意划分方法(记为P )把区间,a b 划分成n 个小区间: y xi-1 xi 图 4-1 O a x1 xn-1 b x ( )yf x 1()if x A B 图 4-2 y ( )yf x xn-1 b x xi-1 xi O a x1 i ( )if § 4-1 柯西-黎曼积分的定义及其性质 143 143 01211iinnaxxxxxxxb 第二步,在每一个小区间上都任意取一点,如在第i 个小区间 ],[1iixx上取的那一点记为i ,做出积分和 121(P;,,,)()i nnnniiifx 1()iiixxx 第三步,让所有小区间都无限变小,即让最大小区间的长度0nx,若有极限 01lim( )ni niixifx 而且与区间的划分方法P 和每一个小区间上那一点(1)iin 的选取方法都无关,则称函数( )f x 在区间,a b 上可积分(简称可积),并称极限值 01lim()( )dni nbiixaifxf x x (4-1) 为函数)(xf在区间ba,上的积分. 上述定义比较长,你可按“划分区间做出积分和取极限”记忆它.请读者注意.....,极限(4-1)不是第1章中说的函数极限,因为其中的积分和12(P;,,,)nnn 不仅与划分区间的方法P 有关,而且也与每个小区间上取的那一点(1)iin 有关.要进一步说明白它,需要用近代极限概念的“...