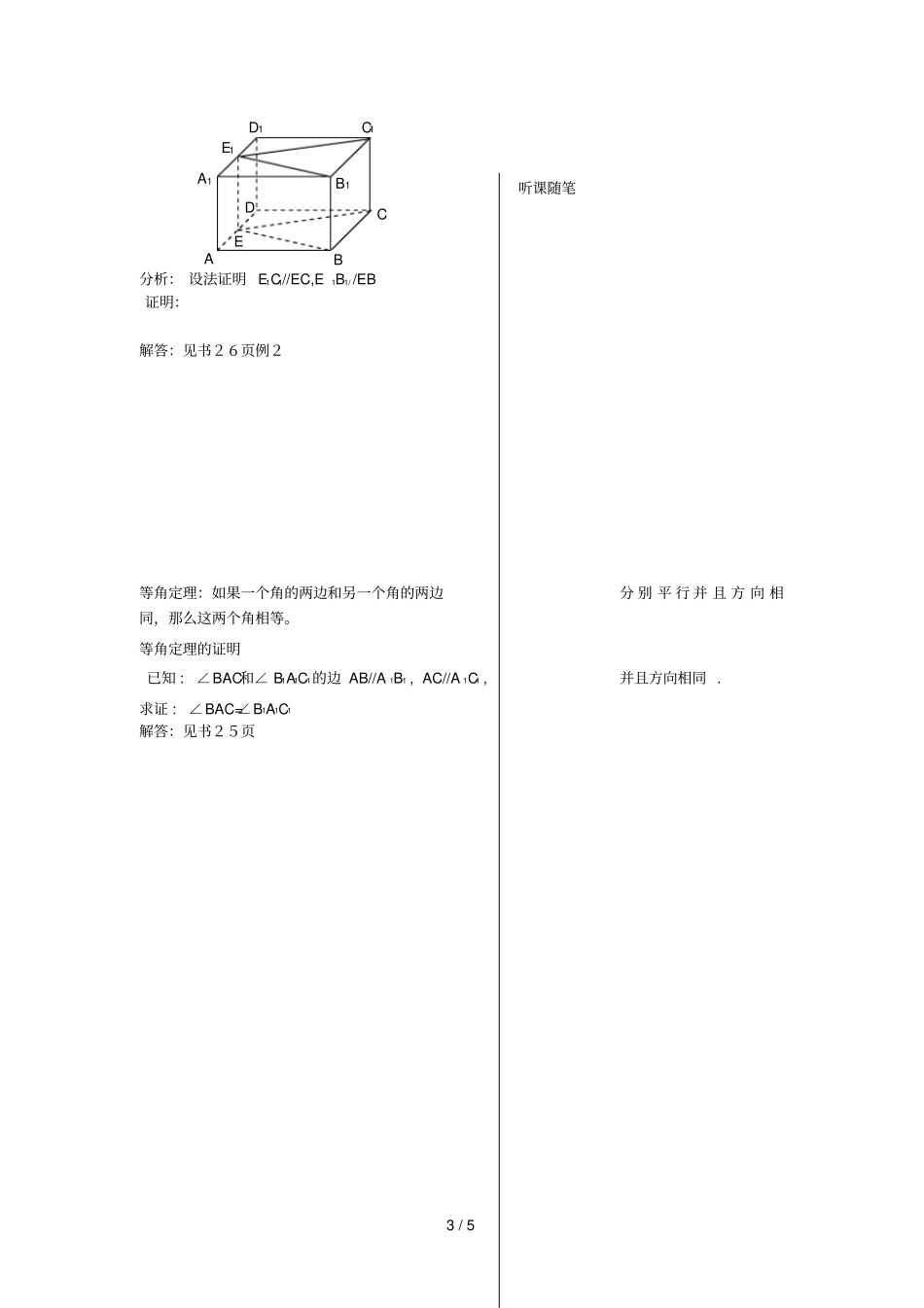
1 / 5 1.2.1 空间两条直线的位置关系一、【学习导航】知识网络学习要求1. 了解空间两条直线的位置关系2. 掌握平行公理及其应用3. 掌握等角定理,并能解决相关问题.【课堂互动】自学评价1. 空间两直线的位置关系位置关系共面情况公共点个数相交直线平行直线异面直线2. 公里4:符号表示:思考:经过直线外一点,有几条直线和这条直线平行答:3.等角定理【精典范例 】例 1:. 如图 , 在长方体 ABCD-A1B1C1D1 中, 已知 E、F 分别是 AB、BC的中点 , 求证 : EF//A 1C1听课随笔空间两条直线位置关系异面直线相交异面直线所成角的计算方法平行直线判定及性质判定及性质A B E F C D A1D1C1B12 / 5 解答:见书25页例1思维点拔:证两直线平行的方法:(1) 利用初中所学的知识(2) 利用平行公理.追踪训练已知:棱长为a 的正方体ABCD-A1B1C1D1中, M,N 分别为 CD,AD 的中点,求证:四边形MNAC是梯形. M N 证明略点评:要证梯形,必须证明有两边平行且相等,平行的证明要善于联想平面几何知识.例 2:如图 . 已知 E、E1 分别为正方体ABCD-A1B1C1D1的棱 AD、A1D1的中点 , 求证 : ∠C1E1B1=∠ CEB . A B C D A1D1C1B1应用3 / 5 分析: 设法证明 E1C1//EC,E1B1/ /EB证明:解答:见书26页例2等角定理:如果一个角的两边和另一个角的两边分 别 平 行 并 且 方 向 相同,那么这两个角相等。等角定理的证明已知 : ∠BAC和∠ B1A1C1的边 AB//A 1B1 , AC//A 1C1 , 并且方向相同 . 求证 : ∠BAC=∠B1A1C1解答:见书25页A B C E D A1D1E1C1B1听课随笔