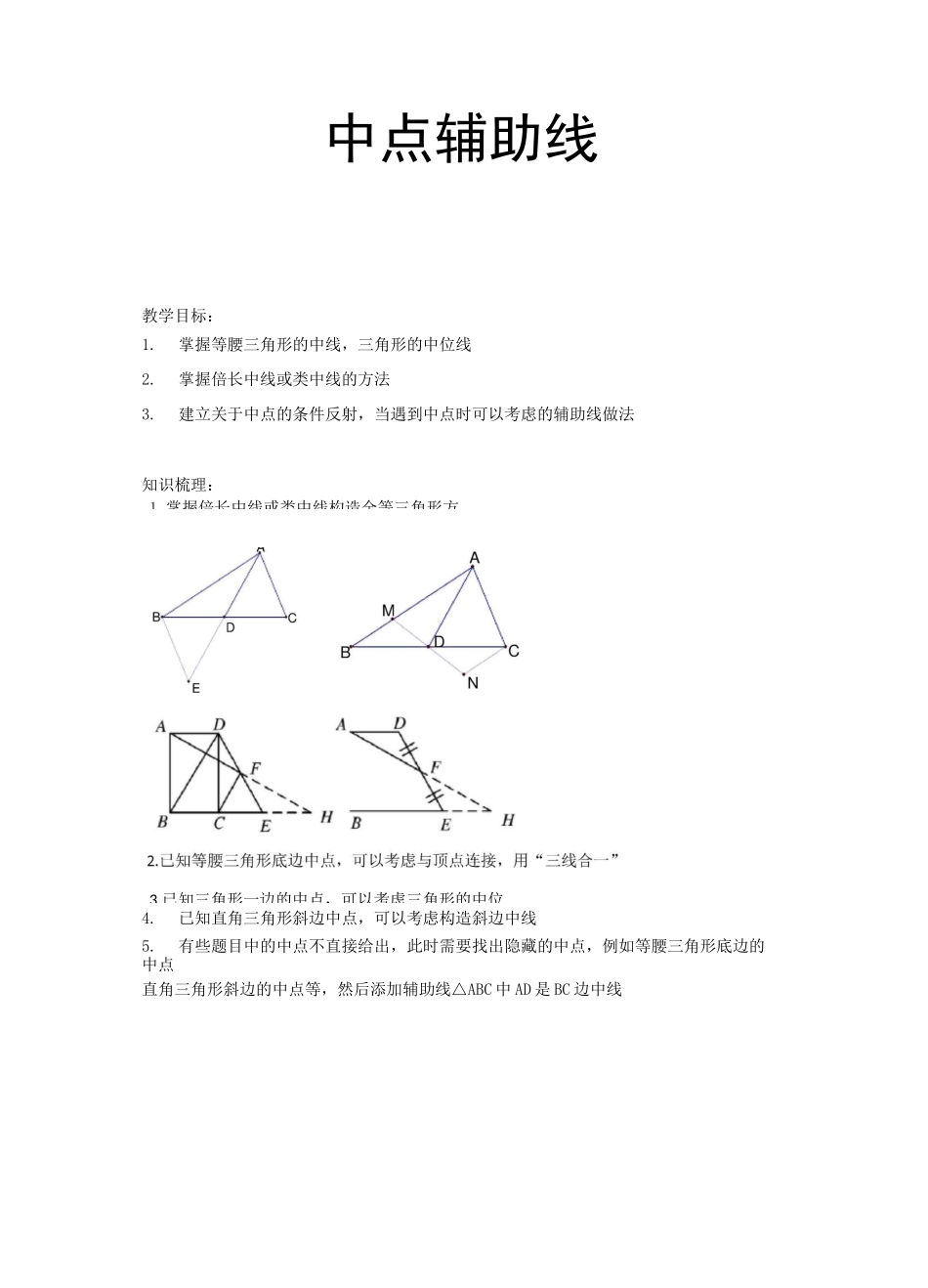
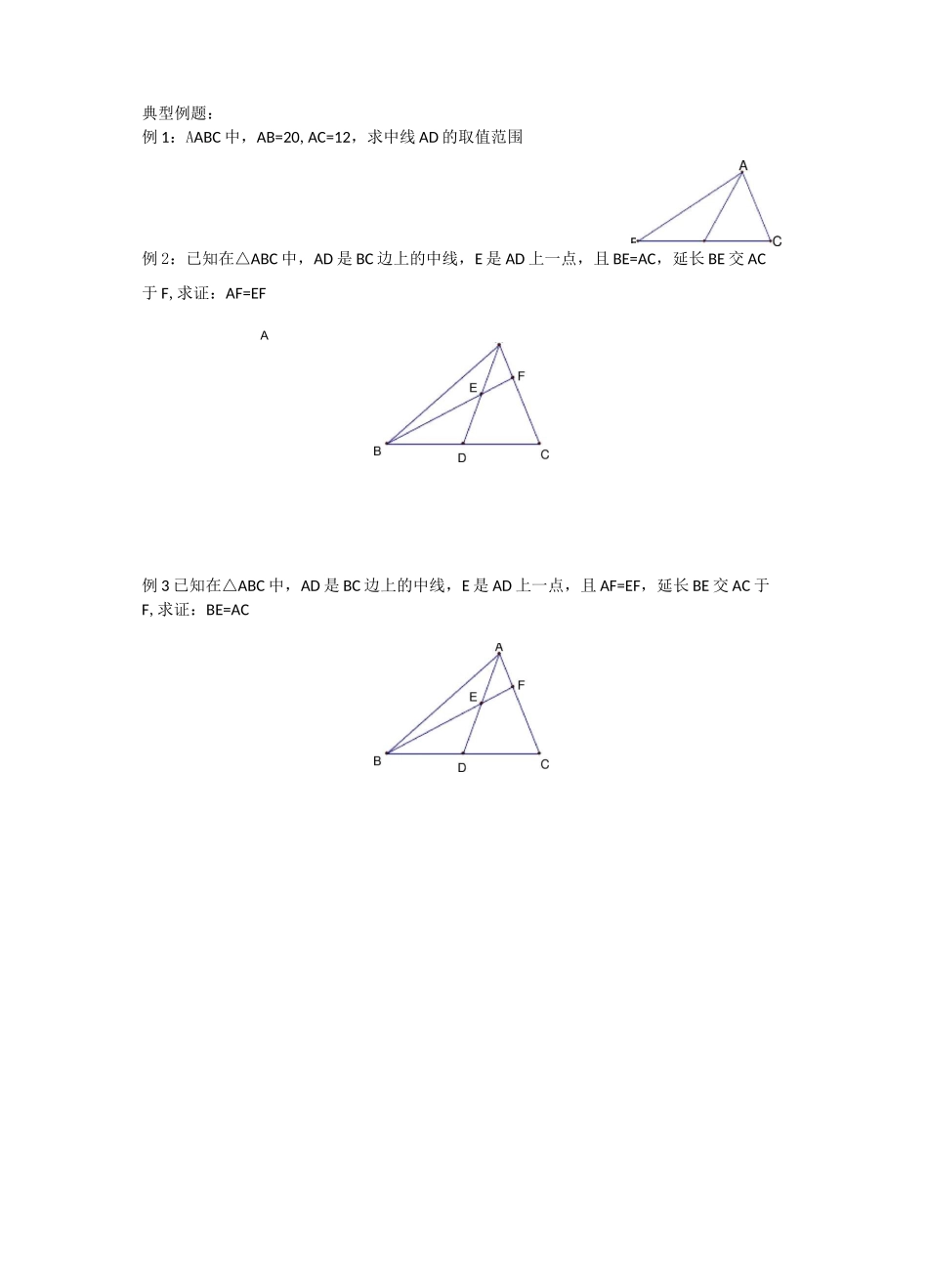
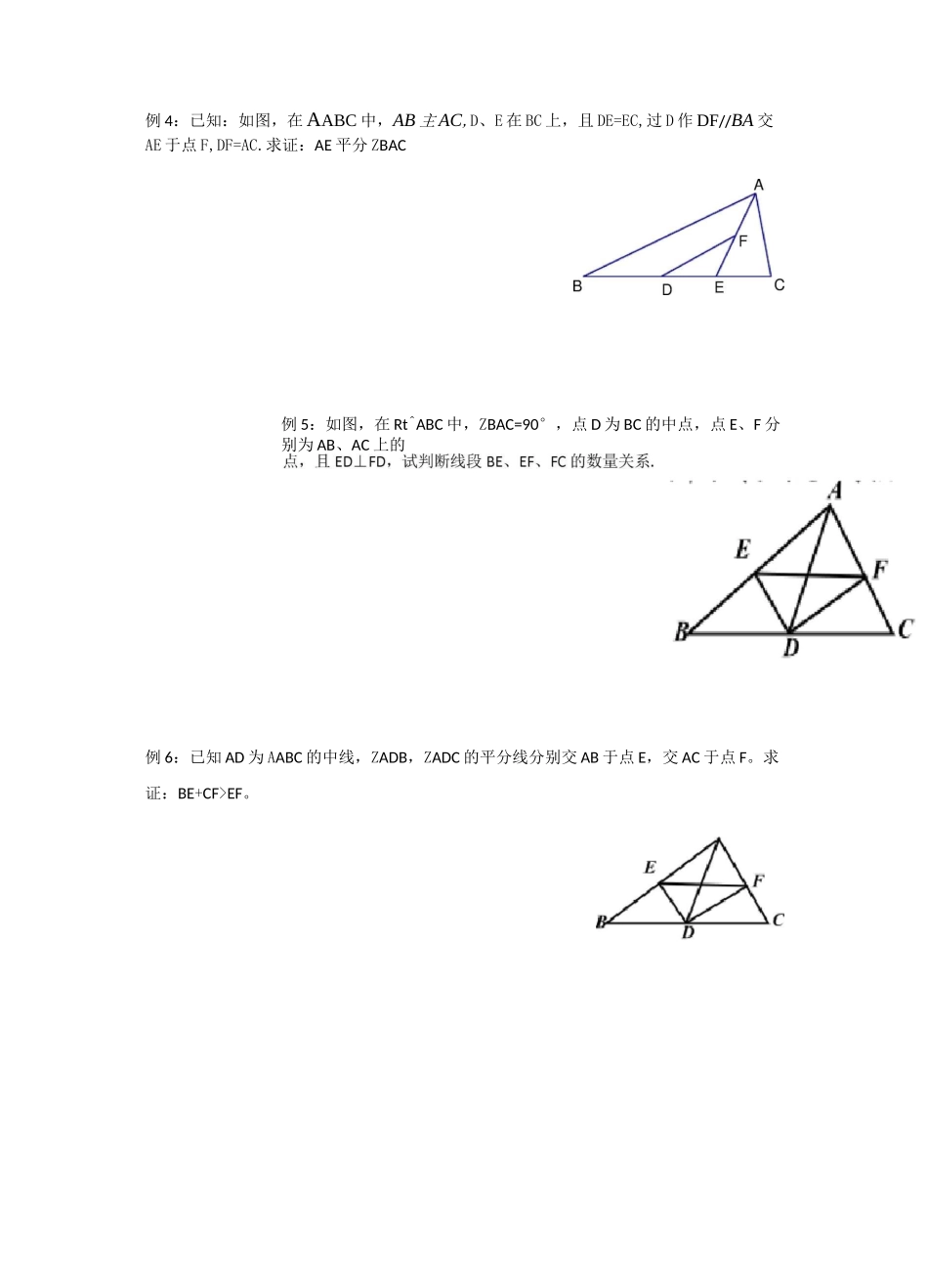
中点辅助线教学目标:1.掌握等腰三角形的中线,三角形的中位线2.掌握倍长中线或类中线的方法3.建立关于中点的条件反射,当遇到中点时可以考虑的辅助线做法知识梳理:4.已知直角三角形斜边中点,可以考虑构造斜边中线5.有些题目中的中点不直接给出,此时需要找出隐藏的中点,例如等腰三角形底边的中点直角三角形斜边的中点等,然后添加辅助线△ABC 中 AD 是 BC 边中线1.掌握倍长中线或类中线构造全等三角形方3.已知三角形一边的中点,可以考虑三角形的中位B典型例题:例 1:AABC 中,AB=20,AC=12,求中线 AD 的取值范围例 2:已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,且 BE=AC,延长 BE 交 AC于 F,求证:AF=EFA例 3 已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,且 AF=EF,延长 BE 交 AC 于F,求证:BE=AC例 4:已知:如图,在 AABC 中,AB 主 AC,D、E 在 BC 上,且 DE=EC,过 D 作 DF//BA 交AE 于点 F,DF=AC.求证:AE 平分 ZBAC例 5:如图,在 Rt^ABC 中,ZBAC=90°,点 D 为 BC 的中点,点 E、F 分别为 AB、AC 上的例 6:已知 AD 为 AABC 的中线,ZADB,ZADC 的平分线分别交 AB 于点 E,交 AC 于点 F。求证:BE+CF>EF。1例 10 问题 1:如图 1,在四边形 ABCD 中,AB=CD,E、F 分别是 BC、AD 的中点,连接 EF 并延长,分别与 BA、CD 的延长线交于点 M、N,求证:ZBME=ZCNE.问题二:如图 2,在四边形 ADBC 中,AB 与 CD 相交于点 0,AB=CD,E、F 分别是 BC、AD 的中点,连接 EF,分别交 DC、AB 于点 M、N,判断 AOMN 的形状,请直接写出结论;问题三:如图 3,在厶 ABC 中,AC>AB,D 点在 AC 上,AB=CD,E、F 分别是 BC、AD 的中点,连接 EF 并延长,与 BA 的延长线交于点 G,若 ZEFC=60°,连接 GD,判断 AAGD 的形状并证明.2当堂练习:1:如图,在△ABC 中,AD 平分 ZBAC,E、F 分别在 BD、AD 上,且 DE=CD,EF=AC,求证:EF〃AB.已知 CD=AB,ZBDA=ZBAD,AE 是△ABD 的中线,求证:ZC=ZBAE3:如图,在△ABC 中,BC=18,BD 丄 AC 于 D,CE 丄 AB 于 E,F、G 分别是 BC、DE 的中点,若 ED=10,则 FG 的长为。AA5:在四边形 ABCD 中,AB〃DC,E 为 BC 边的中点,ZBAE=ZEAF,AF 与 DC 的延长线相交于点F。试探究线段 AB 与 AF、CF 之间的数量关系,并证明你的结论.16:在厶 ...