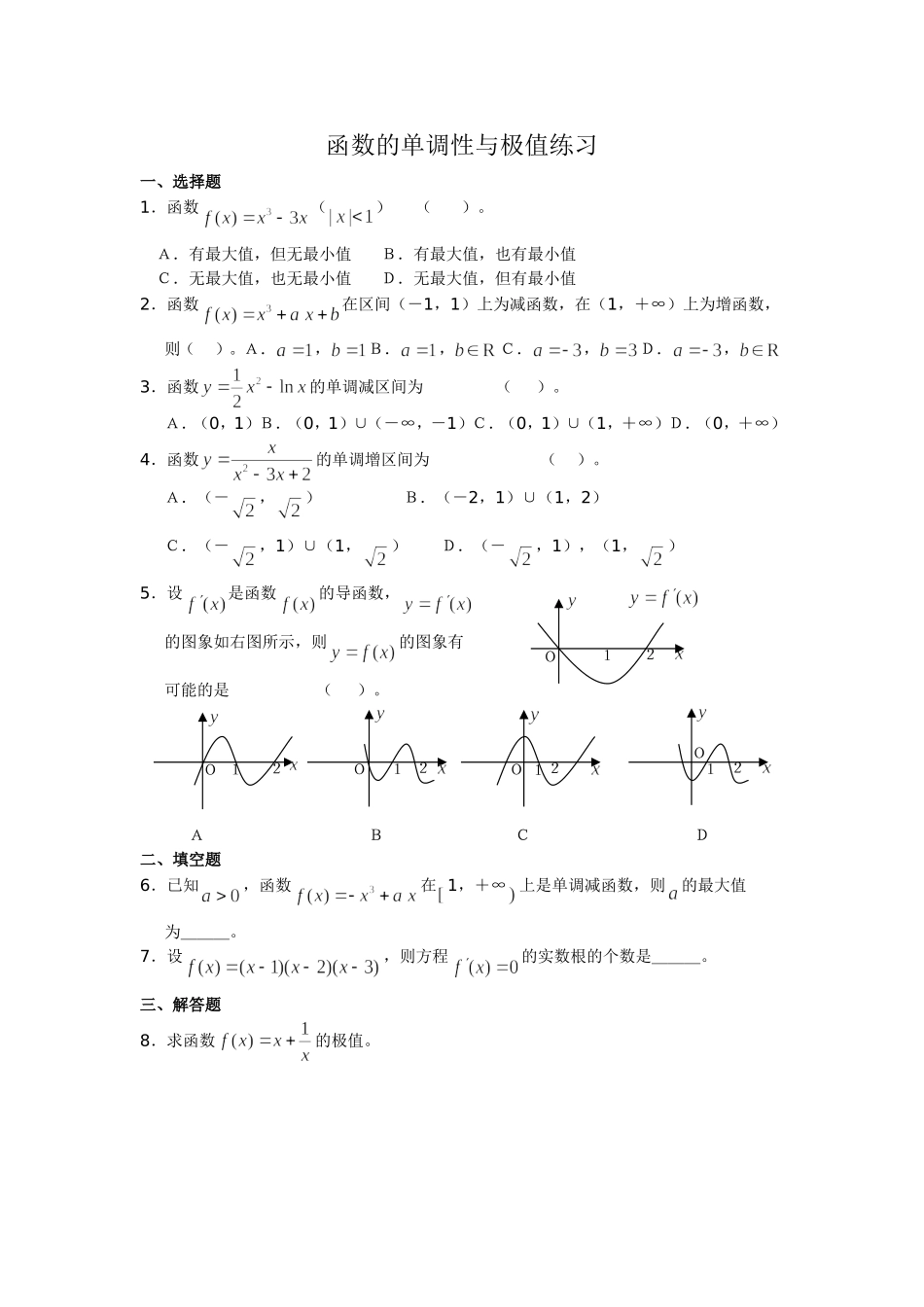
函数的单调性与极值练习一、选择题1.函数()()。A.有最大值,但无最小值B.有最大值,也有最小值C.无最大值,也无最小值D.无最大值,但有最小值2.函数在区间(-1,1)上为减函数,在(1,+∞)上为增函数,则()。A.,B.,C.,D.,3.函数的单调减区间为()。A.(0,1)B.(0,1)∪(-∞,-1)C.(0,1)∪(1,+∞)D.(0,+∞)4.函数的单调增区间为()。A.(-,)B.(-2,1)∪(1,2)C.(-,1)∪(1,)D.(-,1),(1,)5.设是函数的导函数,的图象如右图所示,则的图象有可能的是()。ABCD二、填空题6.已知,函数在1,+∞上是单调减函数,则的最大值为___。7.设,则方程的实数根的个数是___。三、解答题8.求函数的极值。O12OOOO11112222函数的单调性与极值类型一导数与函数的单调性一、选择题1.函数的单调增区间是___。2.若三次函数在区间(-∞,+∞)内是减函数,则a的取值范围___。3.函数在区间(0,1)上的增减性是___。二、填空题4.若函数的单调递减区间为[-1,2],则__,__。5.若函数恰有三个单调区间,则的取值范围是___。6.设(),则的单调增区间为___。7.求函数的单调区间。类型二、函数的极值一、选择题1.函数的极小值点是___。2.函数在区间[-,]上的极大值点为___。3.函数的极大与极小值___。二、填空题4.函数在区间[-2,1]上的最小值为___。5.若函数在R上有两个极值点,则实数的取值范围是___。6.函数在[-,]上的最大值为___,最小值为___。7.已知函数在处取得极值,讨论和是函数的极大值还是极小值。函数的单调性与极值专题1.利用导数判断函数的单调性(1)函数单调性与其导函数的正、负关系在区间(a,b)内,若,则函数y=f(x)在区间(a,b)内单调递增.若,则函数y=f(x)在区间(a,b)内单调递减,若,则函数y=f(x)是常函数,在区间(a,b)内不具有单调性.(2)导数与函数图像的关系若函数在某一区间(a,b)内的导数绝对值较大,则函数在这个范围内变化得快,函数图像比较“陡峭”(向上或向下),反之,函数图像就“平缓”一些.2.求可导函数单调区间的一般步骤与方法(1)确定函数y=f(x)的定义域(2)求,解此方程,求其在定义域内的一切实根.(3)把函数y=f(x)的间断点的横坐标及上面求出的各实根按由小到大的顺序排列,然后用这些点把函数f(x)的定义区间分成若干个小区间.(4)确定在各个小区间的符号,判定函数y=f(x)在每个相应小开区间的单调性.3.函数极值的概念已知函数y=f(x),设是定义域内任意一点,若对附近所有的点x,都有,则称函数y=f(x)在处取极大值,即,称为函数的一个极大值点.反之若,则函数在处取得极小值,即,称为函数的一个极小值点.注意:(1)函数极值是局部性概念,极值点是定义域内的点,而定义域的端点绝不是极值点.(2)若函数y=f(x)在[a,b]内有极值,则函数在区间[a,b]内一定不是单调函数,即给定区间上的单调函数无极值.(3)当函数在区间[a,b]内连续且有有限个极值点时,函数在区间[a,b]内的极大值点与极小值点是交替出现的.4.求函数y=f(x)极值的方法(1)求导数.(2)求方程=0的所有实数根.(3)考察附近的每一个根(从左到右),导函数的符号变化,若的符号由正变负,则是极大值,若的符号由负变正,则是极小值.注意:①可导点不一定是极值点,如,,则x=0不是极值点.故导数为零的点是该点为极值点的必要条件.②不可导点可能是极值点,如,在x=0处不可导,但x=0是函数的极小值点.【典型例题】考点一:判断函数在给定区间上的单调性例1、已知函数,(1)当时,函数在区间(上的单调性如何?(2)当a>0时,判断函数在区间上的单调性.例2、已知函数,讨论函数的的单调性。考点二:求函数的单调区间例3、求函数的单调区间考点三:求函数的极值及其综合应用.例4、求函数的极值0(0,2)2(2,+-0+0-极小值0极大值例5、已知函数f(x)=x3+bx2+cx+2在x=-2和x=处取得极值.(1)确定函数f(x)的解析式(2)求函数f(x)的单调区间;(3)作出函...