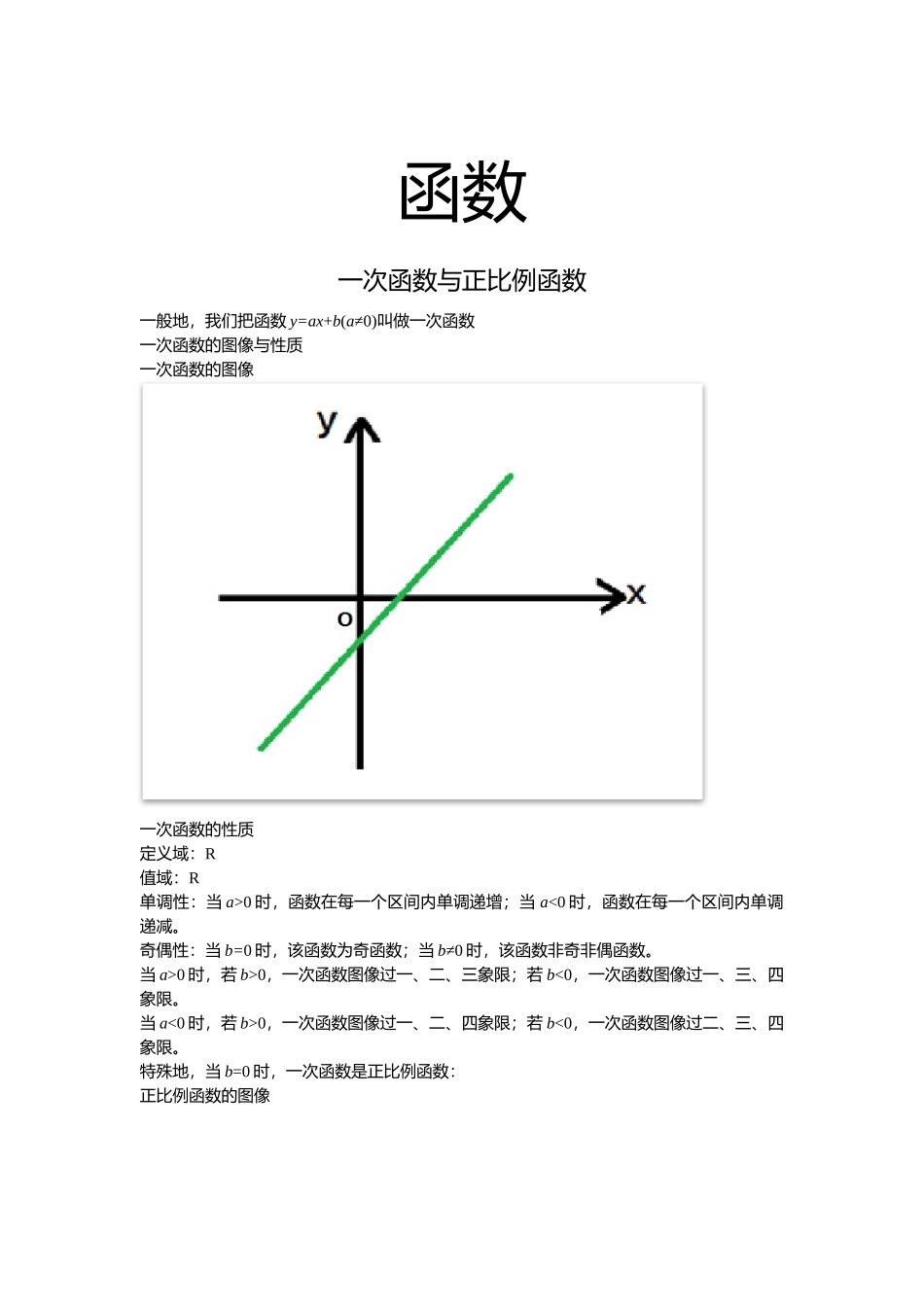
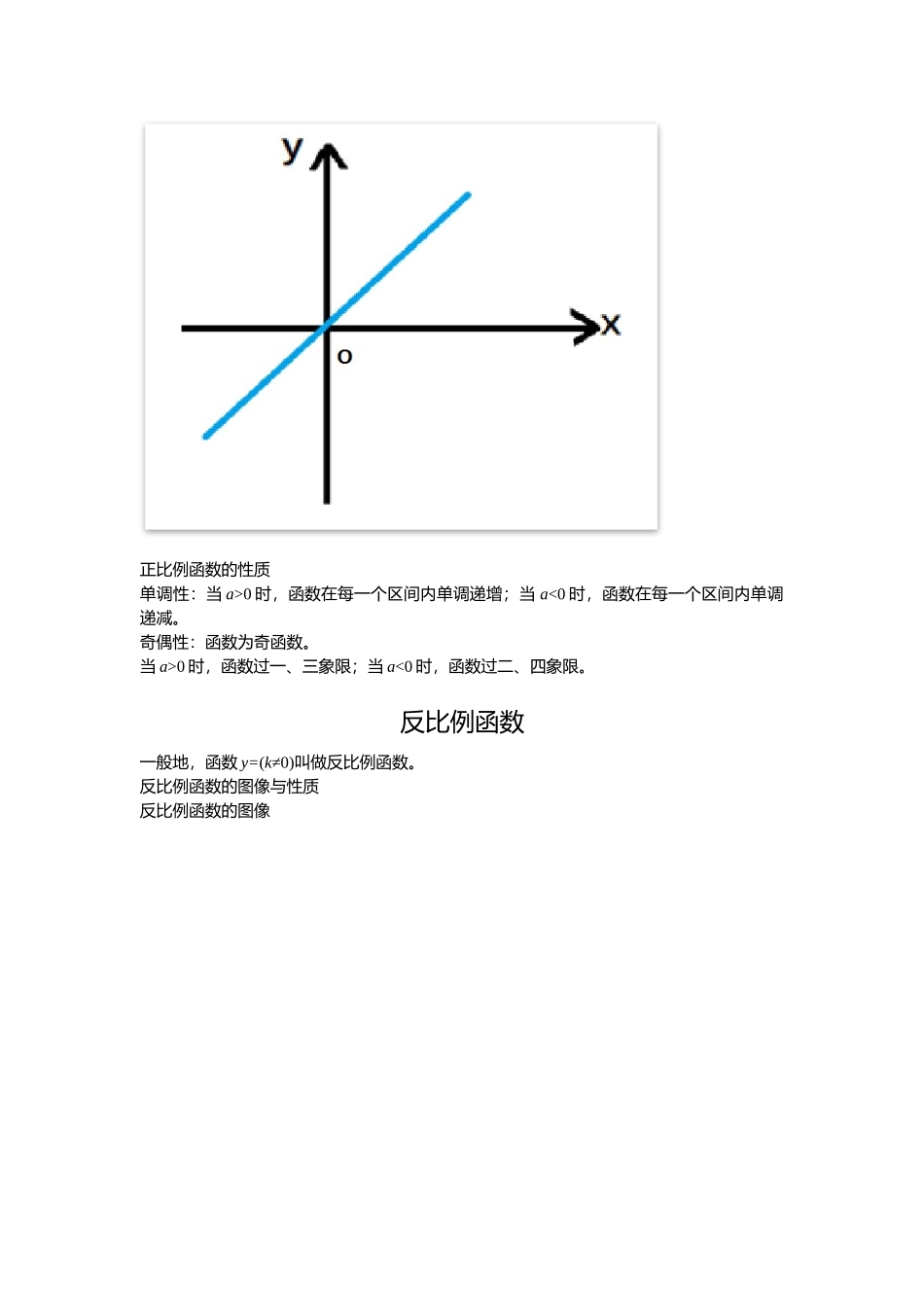
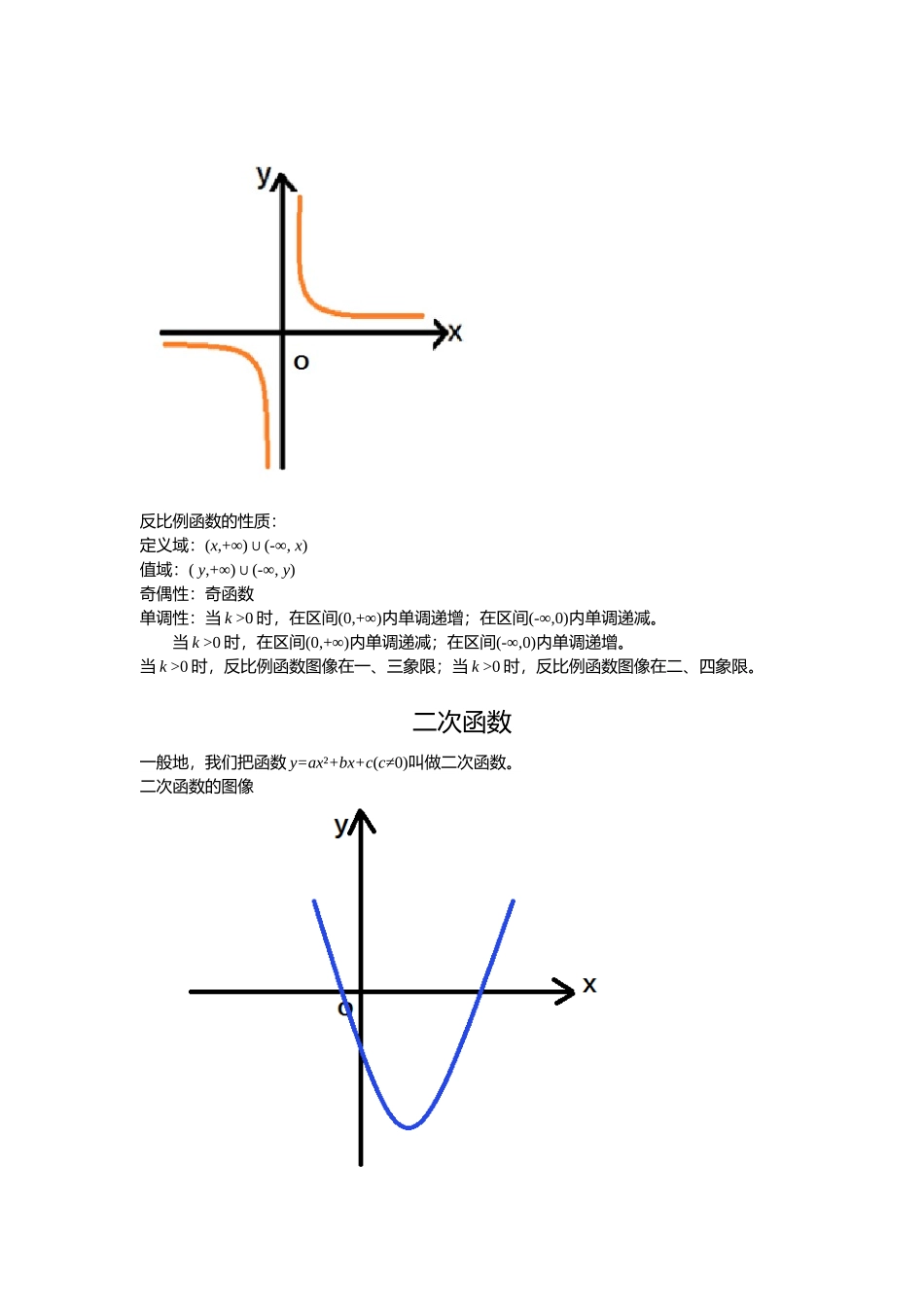
函数一次函数与正比例函数一般地,我们把函数y=ax+b(a≠0)叫做一次函数一次函数的图像与性质一次函数的图像一次函数的性质定义域:R值域:R单调性:当a>0时,函数在每一个区间内单调递增;当a<0时,函数在每一个区间内单调递减。奇偶性:当b=0时,该函数为奇函数;当b≠0时,该函数非奇非偶函数。当a>0时,若b>0,一次函数图像过一、二、三象限;若b<0,一次函数图像过一、三、四象限。当a<0时,若b>0,一次函数图像过一、二、四象限;若b<0,一次函数图像过二、三、四象限。特殊地,当b=0时,一次函数是正比例函数:正比例函数的图像正比例函数的性质单调性:当a>0时,函数在每一个区间内单调递增;当a<0时,函数在每一个区间内单调递减。奇偶性:函数为奇函数。当a>0时,函数过一、三象限;当a<0时,函数过二、四象限。反比例函数一般地,函数y=(k≠0)叫做反比例函数。反比例函数的图像与性质反比例函数的图像反比例函数的性质:定义域:(x,+∞)(-∞,∪x)值域:(y,+∞)(-∞,∪y)奇偶性:奇函数单调性:当k>0时,在区间(0,+∞)内单调递增;在区间(-∞,0)内单调递减。当k>0时,在区间(0,+∞)内单调递减;在区间(-∞,0)内单调递增。当k>0时,反比例函数图像在一、三象限;当k>0时,反比例函数图像在二、四象限。二次函数一般地,我们把函数y=ax²+bx+c(c≠0)叫做二次函数。二次函数的图像二次函数的性质定义域:R值域:R二次函数的对称轴:x=-二次函数的顶点:(-,)抛物线开口情况:当a>0时,二次函数的开口向上;当a<0时,二次函数的开口向下。二次函数的单调性:当a>0时,二次函数在区间[-,+∞)内单调递增;在区间(-∞,-]内单调递减。当a<0时,二次函数在区间(-∞,-]内单调递增;在区间[-,+∞)内单调递减。二次函数的奇偶性当b=c=0时,二次函数为偶函数;其它的是非奇非偶函数。二次函数的最值当a>0,x=-时,函数有最小值f(-);当a<0,x=-时,函数有最大值f(-)。指数函数一般地,函数y=ax(a>0,且a≠1)叫做指数函数。指数函数的图像指数函数的性质定义域:R值域:(0,+∞)函数在x轴的上方,且过点(0,1)。单调性:a>1时,函数单调递增;若0
0,且a≠1)叫做对数函数。对数函数的图像对数函数的性质定义域:(0,+∞)值域:R函数在x轴的右方,且过点(1,0)。单调性:a>1时,函数单调递增;若00时,函数在区间(0,+∞)上单调递增;a<0时,函数在区间(0,+∞)内单调递减。都过点(1,1)a>0时,函数过原点。讨论指数为有理数的幂函数y=xa(a∈Q,|a|=,,m,n∈N+)为有理数指数幂函数。n=偶数时,函数在区间(-∞,0)内没有定义。奇偶性:n为奇数,m为偶数,该函数为偶函数。n为奇数,m为奇数,该函数为偶函数。对勾函数一般地,函数y=ax+(a,,b>0)叫做对勾函数。对勾函数的图像对勾函数的性质定义域:(x,+∞)(-∞,∪x)值域:R单调性:在区间(-∞,)与区间(,+∞)内单调递增;在区间(,0)与区间(0,)内单调递减。奇偶性:奇函数三角函数正弦函数的图像与性质一般地,函数y=sinx叫做正弦函数。正弦函数的图像正弦函数的性质定义域:R值域:[-1,1]最小正周期:2π奇偶性:奇函数单调性:在区间[2k-,2kπ+]内单调递增;在区间[2kπ+,2kπ+]单调递减。对称轴:x=kπ+对称中心:(kπ,0)余弦函数的图像与性质一般地,函数y=cosx叫做余弦函数。余弦函数的图像余弦函数的性质定义域:R值域:[-1,1]最小正周期:2π奇偶性:偶函数单调性:在区间[2kπ-π,2kπ]内单调递增;在区间[2kπ,2kπ+π]单调递减。对称轴:x=kπ对称中心:(kπ+,0)正切函数的图像与性质一般地,函数y=tanx叫做正切函数。正切函数的图像正切函数的性质定义域:[x|x≠kπ+]值域:R最小正周期:π奇偶性:奇函数单调性在每一个开区间(-kπ,-+kπ)内都是增函数。对称轴:x=kπ+对称中心:(kπ,0)几...