真实应力应变曲线VIP免费

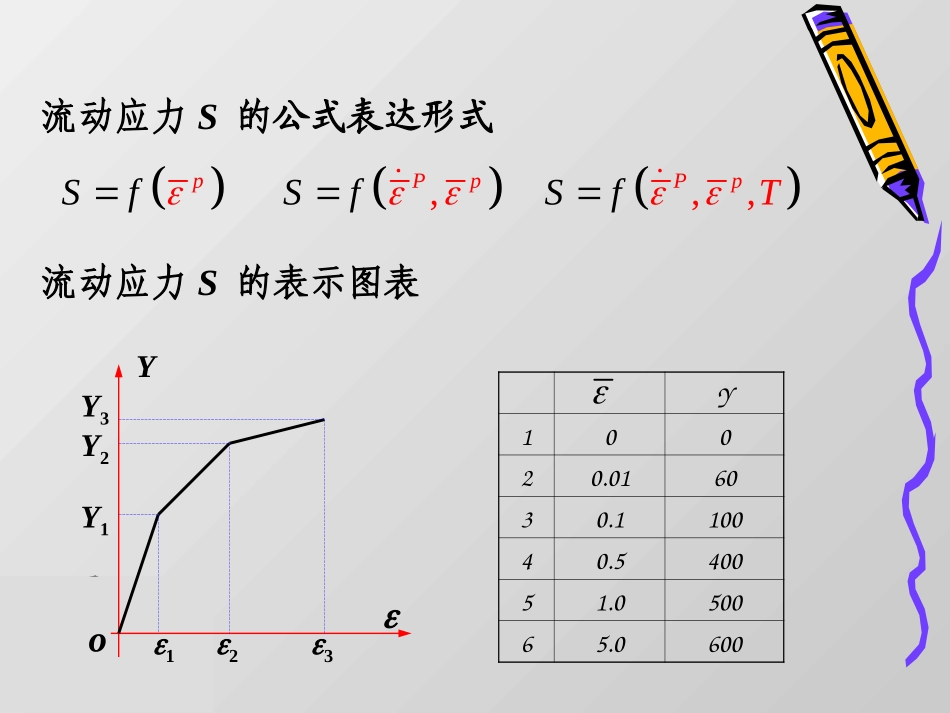
§3.6真实应力－应变曲线应力－应变曲线反映变形体变形时应力随应变强化的规律。初始屈服应力S一般屈服应力(流动应力S,Y)真实应力：变形体内实际承受应力的大小。影响流动应力的因素材料属性，温度，应变，应变速率建立真实应力－应变曲线方法拉伸试验，压缩试验，扭转试验,,PpTSf,PpSfpSf流动应力S的公式表达形式Yo123Y1Y2Y3Y10020.016030.110040.540051.050065.0600流动应力S的表示图表一、拉伸试验曲线单向拉伸，。1123123,0;,2111、拉伸图和条件应力－应变曲线弹性伸长变形→屈服→均匀塑性变形→塑性失稳→断裂00AF0ll三个变形阶段：弹性变形屈服→均匀塑性变形塑性失稳→断裂特征点：弹性极限点p，屈服点c，失稳点b，断裂点k。bkdcpohgF(0)Δl()FdFcFpFb=Fmax?用真实应力与应变表示的曲线。();();()SSS2、真实应力－应变曲线0011FFSAAln11bbbSln1bb断裂点k，0;lnkkkkkFASAAzz齐别尔(Siebel)修正'''18kkSSd0AFSASe3、拉伸真实应力－应变曲线在塑性失稳点的特性失稳点b，Fb=Fmax。000lnlnAAlAlAe0ddd0FAeSSedd0SSddbbSS二、压缩试验曲线拉伸试验曲线：失稳，精确范围（<0.3）；压缩试验曲线：摩擦（S），精确范围（2）；1、直接消除摩擦的圆柱体压缩法0PPSAAe0lnHH2、外推法摩擦力影响和式样尺寸D0/H0有关，根据不同的D0/H0，外推出D0/H0=0时的S，得到真实应力－应变曲线。三、真实应力－应变曲线的简化形式1、密指数硬化曲线nSBnbbSB1ddnbbbSnBS;bbbbSnB★,,TSf,SfSf真实应力－应变曲线的公式表达形式nScasnSknSk2、有初始屈服应力的密指数硬化曲线1mSSB3、有初始屈服应力的刚（弹）塑性线性硬化曲线2sSB21SBB4、理想刚（弹）塑性线性硬化曲线sSnpSca四、包申格效应(Bauschingereffect)包申格效应—随加载路径和方向不同，屈服应力降低的现象。（随动强化）实际应用：冷镦效应消除：缓慢退火例3-11应力应变曲线的应用受内压薄壁圆筒，半径r=200mm，内压p=10Mpa，壁厚t=4mm，真实应力应变曲线，求壁厚减薄量。0.25800S123;;02zprprtt22212233112110200634332242prMPaMPat13平面应变问题2221223311123261.15530.25800S0.2518001.154433.714tmm331374.310;74.31033074.310lntt043.7140.286tttmmmm