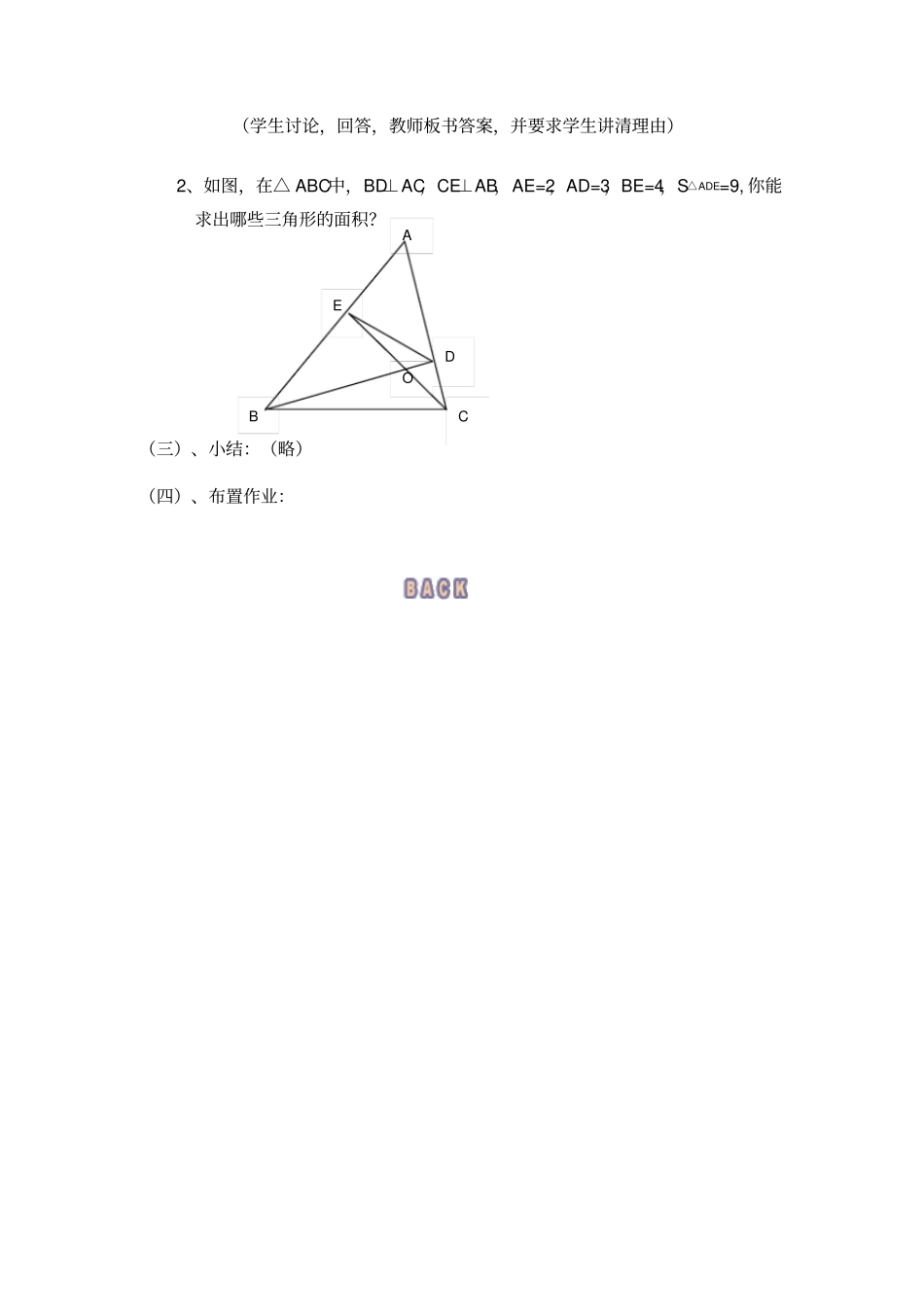
相似三角形的面积比与相似比的关系执教老师:园南中学姚春花一、教学目标:1、掌握“相似三角形的面积比等于相似比的平方”,并会应用结论解决问题;2、培养学生对数学结论的公理化的论证能力;3、通过例题的分析、研究,培养学生的发散性思维;4、通过认知冲突激发学生的学习兴趣,使学生主动活泼、自主、自动地进行学习,让学生获得成功的喜悦。二、教学重点和难点 :“相似三角形的面积比等于相似比的平方”,并会应用结论解决问题;三、教学过程:(一)、创设情景、引入新课1、已知:在△ ABC中,∠ABC=90o,D、E 分别在 AB、AC上,DE∥BC,AD∶AB=1∶3,AD=3,DE=4,求 S△ADE∶S△ABC的值。2、如果把上题中的阴影部分条件换成AD=a,DE=b呢?3、如果上题中的△ ABC换成一般三角形呢?4、如果上题中 AD∶AB=K呢?结论:相似三角形的面积的比等于相似比的平方(学生口述,教师板演过程)(二)、定理应用A、简单应用:A D E B C A D E B C 1、如果两个三角形相似,其中一组对应边分别是3 和 4,那么它们的面积比是2、已知两个三角形相似,面积比是1∶2,则相似比是3、如果把一个三角形的三条边的长都扩大为原来的100 倍,那么这个三角形的面积扩大为原来的多少倍?4、如果把一个三角形的面积扩大为原来的100 倍,且与原三角形相似,那么这个三角形的边长扩大为原来的多少倍?B、应用举例在 ABCD 中,延长 BC到 E,使 CE∶BC=1∶2,连接 AE交 DC于 F,求证: S △AFD ∶ S△EFC=4∶1C、变式练习:1、 如图,在△ ABC中, DE∥BC,DE交 AB、AC于点 D、E,1) 、若 AD∶BD=1∶2,S △ADE∶S△ABC=______, 2) 、若 DE=2,BC=5,=20,求:3) 、若 AD∶DB=2∶3,S 四边形 DBCE=12,求 S△ABC4) 、若 DE=2,BC=5,连结 BE、CD交于点 O,=4,问在图形中可求出哪些三角形的面积?F B C E A D O A B C D E (学生讨论,回答,教师板书答案,并要求学生讲清理由)2、如图,在△ ABC中,BD⊥AC,CE⊥AB,AE=2,AD=3,BE=4,S△ADE=9, 你能求出哪些三角形的面积?(三)、小结:(略)(四)、布置作业:A B C E D O