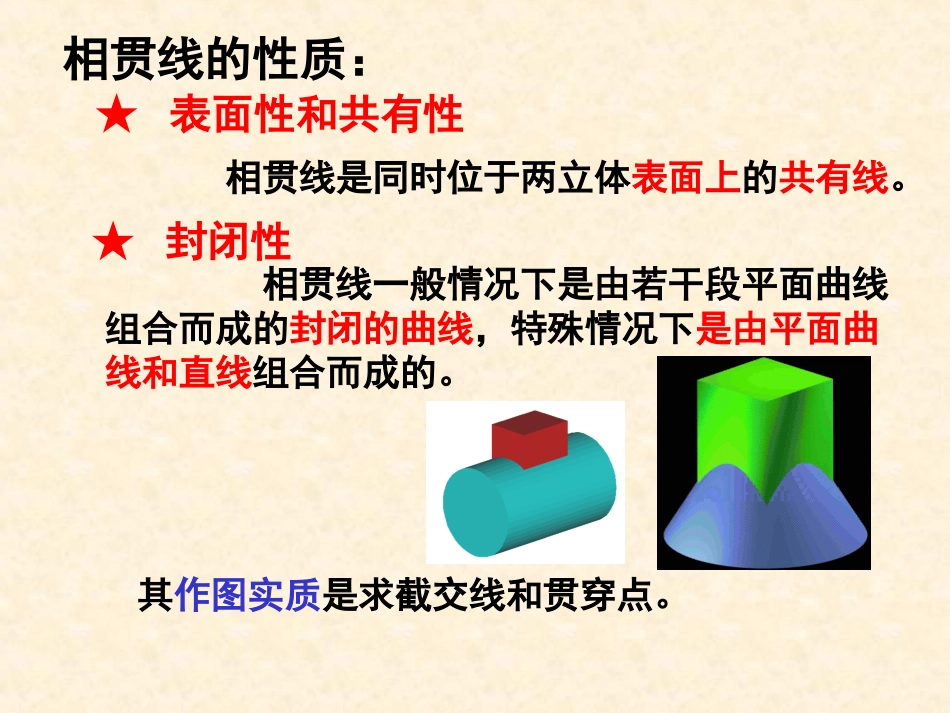
§7-4平面体与曲面体相贯§7-5两曲面体相贯平面体与回转体相贯回转体与回转体相贯多体复合相贯立体相贯的形式:两立体相交叫作相贯,其表面产生的交线叫做相贯线。本节主要讨论轴线垂直某一投影面的常见回转体(圆柱、圆锥、球)与平面体相交,且相贯线至少有一个投影已知时,其相贯线的性质、投影特性及作图方法。平面体与平面体相贯§7-4平面体与曲面体相贯相贯线的性质:其作图实质是求截交线和贯穿点。★表面性和共有性相贯线是同时位于两立体表面上的共有线。★封闭性相贯线一般情况下是由若干段平面曲线组合而成的封闭的曲线,特殊情况下是由平面曲线和直线组合而成的。例1:求四棱柱和圆锥的相贯线。1、求贯穿点;2、求中间点;3、依次平滑连接各点;4、整理投影图。例2:求三棱柱与圆锥的相贯线。1、求贯穿点;2、求中间点;3、依次平滑连接各点;4、整理投影图。例3:补全四棱柱与圆柱的相贯线。21(2')1'3'33"1"2"4'(5')455"4"例4:补全四棱柱与圆柱的投影。§7-5曲面立体相贯回转体与回转体相贯•圆柱与圆柱相贯•圆柱与圆锥相贯•圆柱与圆球相贯•圆锥与圆球相贯1、回转体相贯的三种基本形式外表面与内表面相交两外表面相交两内表面相交本节主要讨论常见回转体(圆柱、圆锥、球)轴线正交时,其相贯线的性质、投影特性及作图方法。2.相贯线主要性质其作图实质是找出相贯的两立体表面的若干共有点的投影。★表面性和共有性相贯线是两立体表面的共有线。相贯线上的点是两立体表面的共有点。★封闭性两回转体的相贯线一般情况是封闭的空间曲线,特殊情况下是平面曲线或直线。回转体相贯线的性质——图例3、求回转体相贯线的方法1)表面取点法:适用于相贯两立体中至少有一个圆柱(即至少一个投影有积聚性)时。2)辅助(平)面法:多用于相贯两立体的投影都不具有积聚性时。利用辅助平面法求相贯线的作图方法辅助平面的选择原则:假想用辅助平面截切两回转体,分别得出两回转体表面的截交线。由于截交线的交点既在辅助平面内,又在两回转体表面上,因而是相贯线上的点。根据三面共点的原理。4、求相贯线的一般步骤:4.判别可见性,光滑且顺次地连接各点,作出相贯线;5.整理轮廓线。确定交线的弯曲趋势确定交线的范围2.求作相贯线上的特殊点;3.根据需要求出若干个一般点;1、空间和投影分析(1)分析两回转体的几何形状、相对大小和相对位置;(2)分析两回转体对投影面的相对位置,哪个投影有积聚性,找出已知投影,预测未知投影;5、复合相贯线三个或三个以上的立体相交在一起,称为复合相贯。这时相贯线由若干条相贯线组合而成,结合处的点称为结合点。当两个回转体具有公共轴线时,其表面的相贯线为圆,且该圆平面垂直于公共轴线。当公共轴线处于投影面垂直位置时,相贯线有一个投影反映圆的实形,其余投影积聚为直线。6.相贯线的特殊情况(一)斜交正交正交6.相贯线的特殊情况(二)斜交外切于同一球面的两圆柱相交,其相贯线为两条平面曲线—椭圆。外切于同一球面的圆锥、圆柱相交时,其相贯线为两条平面曲线—椭圆。当相交两立体的轴线同时平行于某一投影面时,则此两椭圆曲线在该投影面上的投影,为相交两直线。当相贯两圆柱的轴线平行或相贯两圆锥共一顶点时,相贯线是直线。6.相贯线的特殊情况(三)相贯线向大圆柱轴线一侧弯交线为两条平面曲线(椭圆)当圆柱的相对大小发生变化时,相贯线的变化趋势相贯线向大圆柱轴线一侧弯7、相贯线的变化趋势一圆柱与圆锥相贯线的变化趋势当大小发生相对变化时,圆柱与圆锥相贯线的变化趋势7、相贯线的变化趋势二yyyyded'e'a'c'b'a"b"c"d"e"bac1、分析相贯线的水平投影和侧面投影已知,可利用积聚性,采用表面取点法求共有点;可见性的判断原则:同时位于两立体的可见表面上时,为可见;否则,为不可见。2、求出相贯线上的特殊点A、B、C;3、求出若干个一般点D、E;4、判别可见性,光滑且顺次地连接各点,作出相贯线;5、整理轮廓线。例1:求两圆柱的相贯线。注意:在两体相交区域内不应有圆柱体轮廓线的投影。解题步骤例2:圆柱与圆锥相贯,求其相贯线的投影。◆空间及投影分析:相贯线为一光滑的封闭的空间曲线。它的侧...