2019四川中考数学考前专题训练二次函数综合题10道

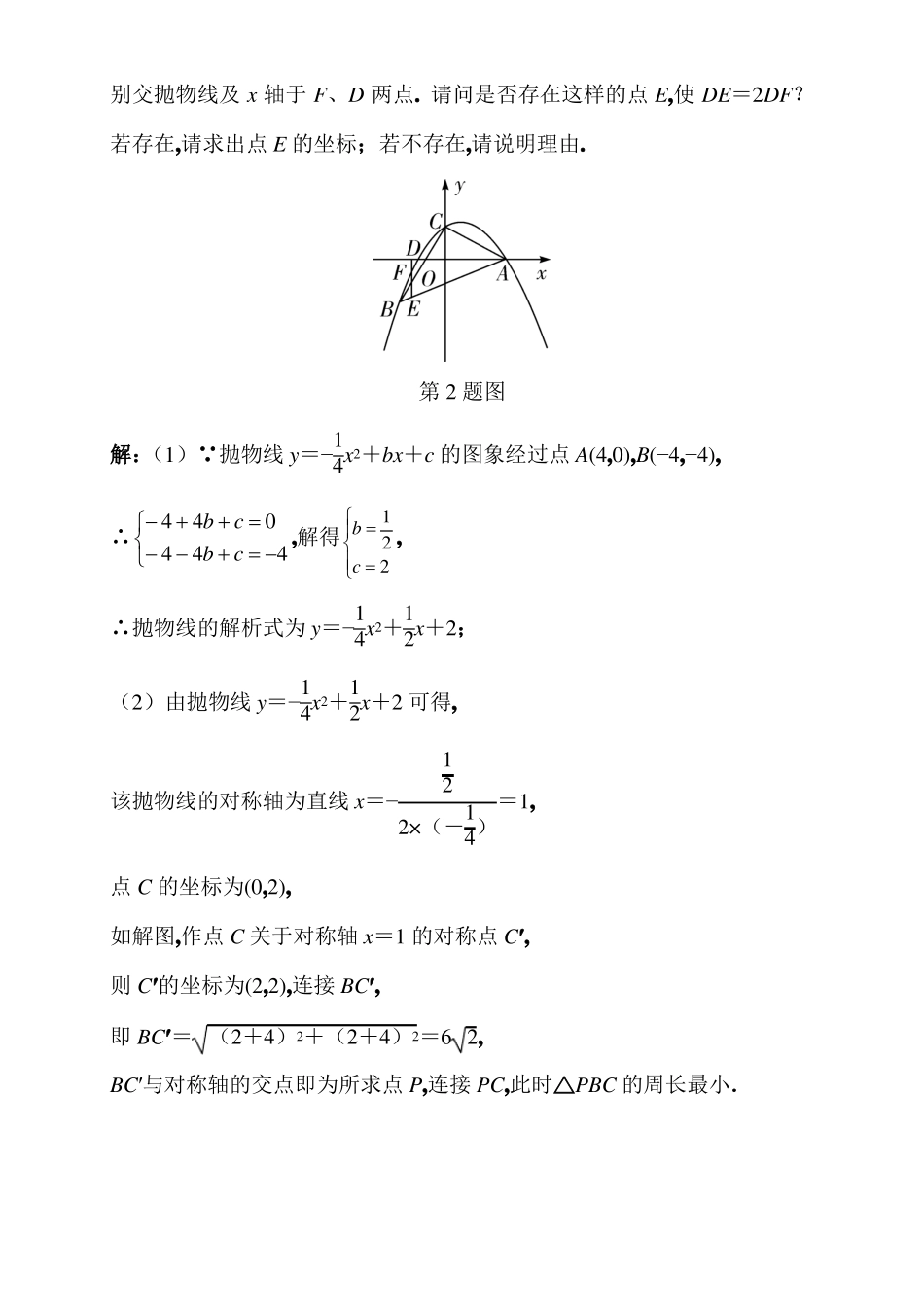
题型五二次函数综合题类型一线段数量关系与最值关系1.如图,抛物线 y＝x2＋bx＋c 过点 A(3,0), B(1,0),交 y 轴于点 C,点 P 是该抛物线上一动点,点 P 从 C 点沿抛物线向 A 点运动(点 P 不与点 A 重合),过点 P作 PD∥y 轴交直线 AC 于点 D.(1)求抛物线的解析式;(2)求点 P 在运动的过程中线段 PD 长度的最大值;(3)在抛物线对称轴上是否存在点 M,使|MA－MC|最大？若存在,请求出点 M的坐标;若不存在,请说明理由．解：（1） 抛物线 y=x2+bx+c 过点 A（3,0）,B（1,0）,93b  c  0b  4∴ ,解得,1b  c  0c  3∴抛物线解析式为 y=x2﹣4x+3;（2）x=0,则 y=3,∴点 C（0,3）,令则直线 AC 的解析式为 y=−x+3,设点 P（x, x2−4x+3）, PD∥y 轴,∴点 D（x,−x+3）,∴PD=（−x+3）−（x2−4x+3）=−x2+3x=−（x−）2+, a=−1＜0,3294∴当 x=时,线段 PD 的长度取最大值,最大值为;（3）存在.由抛物线的对称性得,对称轴垂直平分 AB,∴MA=MB,当 M、B、C 不在同一条直线上时,由三角形的三边关系得,|MA−MC|=|MB−MC|＜BC,当 M、B、C 三点共线时,|MA−MC|=|MB−MC|=BC,∴|MA−MC|≤BC,即当点 M 在 BC 的延长线上时,|MA−MC|最大,最大值即为 BC 的长度,设直线 BC 的解析式为 y=kx+b（k≠0）, B（1,0）,C（0,3）,3294k  3k b  0则 ,解得,b  3b  3∴直线 BC 的解析式为 y=−3x+3, 抛物线的对称轴为 x=2,∴当 x=2 时,y=−3×2+3=−3,∴点 M（2,−3）,即抛物线对称轴上存在点 M（2,−3）,使|MA−MC|最大．2.如图,抛物线 y＝−x2＋bx＋c 的图象过点 A（4,0）,B（−4,−4）,且抛物线与 y 轴交于点 C,连接 AB,BC, AC.(1)求抛物线的解析式；(2)点 P 是抛物线对称轴上的点,求△PBC 周长的最小值及此时点 P 的坐标；(3)若 E 是线段 AB 上的一个动点(不与 A、B 重合),过 E 作 y 轴的平行线,分14别交抛物线及 x 轴于 F、D 两点. 请问是否存在这样的点 E,使 DE＝2DF？若存在,请求出点 E 的坐标；若不存在,请说明理由.第 2 题图12解：（1） 抛物线 y＝−4x ＋bx＋c 的图象经过点 A(4,0),B(−4,−4),1 4  4b  c  0b ∴,解得2 , 4  4b  c  4c  2121∴抛物线的解析式为 y＝−4x ＋2x＋2；11（2）由抛物线 y＝−4x2＋2x＋2 可...