图上的距离与实际距离VIP免费

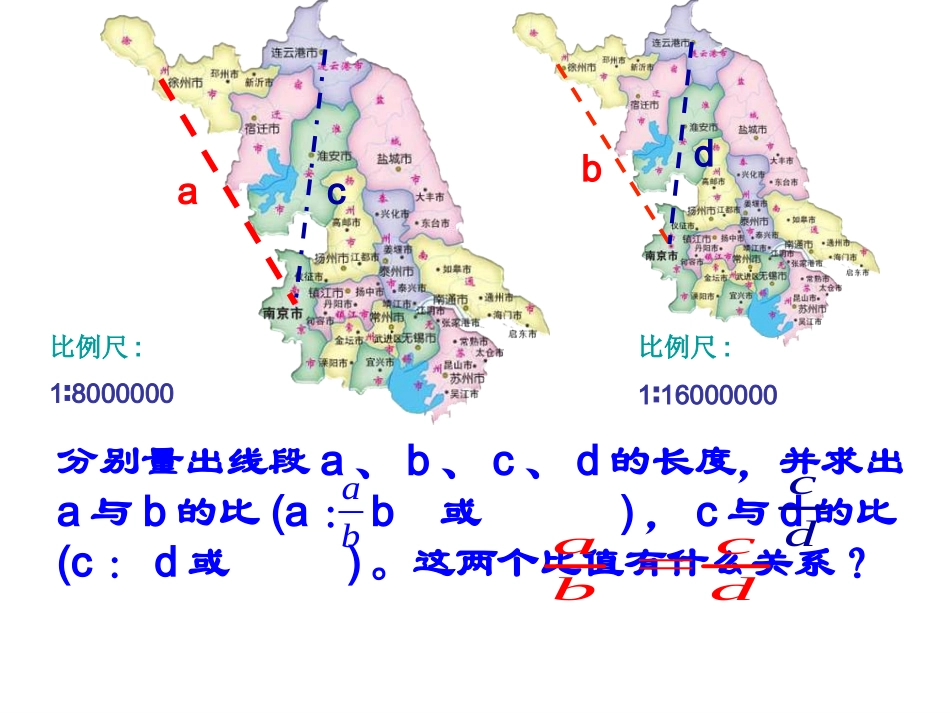
初中数学八年级下册（苏科版）10.1图上距离与实际距离10.1图上距离与实际距离比例尺:18000000∶比例尺:116000000∶abcd分别量出线段a、b、c、d的长度，并求出a与b的比(a：b或)，c与d的比(c：d或)。这两个比值有什么关系？abcdacbd•线段的比：在同一单位长度下，两条线段长度的比叫做这两条线段的比。成比例线段：在4条线段中，如果两条线段的比等于另外两条线段的比，那么称这4条线段成比例。（如果线段a、b、c、d满足a∶b=c∶d或，那么称线段a、b、c、d成比例）吃透概念吃透概念acbd其中：a、b、c、d叫做组成比例的项，线段a、d叫做比例外项，线段b、c叫做比例内项，线段d叫做a、b、c的第四比例项；（1）线段的比（2）成比例线段1、完成下列各组练习，并谈谈你是怎样理解“线段的比”这一概念的.（1）判断：①两条线段的比与数的比一样有正有负（）②两条线段的比是指它们长度的比（）③两条线段的比与它们采用的单位有关（）合作交流2、什么叫成比例线段，并谈谈你是怎样理解这一概念的.合作交流（1）成比例线段是4条线段之间的关系，它揭示的是两组线段比之间的相等关系；（2）成比例线段是用“＝”连接比值相等的两组线段，它是一个等式，具有等式的一切性质；（3）线段a、b、c、d成比例亦可说a、b、c、d是成比例线段.剖析：问题:线段a的长度为3cm,线段b的长度为6m,那么这两条线段的比为.在求两条线段的比时,如果单位不同,必须先化成同一单位,再求它们的比.试一试1、兴华机械厂要加工一种精密零件，该零件长30mm，现要把它放大画在图纸上，若按照比例尺为10：1，那么该零件在图纸上有＿＿＿＿cm2、线段AB＝0.2cm，CD＝10cm，则AB：CD＝＿＿＿＿＿3、若a、b、d、c是成比例线段，其中a＝5cm，b＝3cm，c＝2cm，则线段d＝＿＿＿＿＿cm分层训练（（11）下列各组线段中，长度成比例的（）下列各组线段中，长度成比例的（））AA、、22㎝㎝、、33㎝㎝、、44㎝㎝、、11㎝㎝BB、、1.51.5㎝㎝、、2.52.5㎝㎝、、6.56.5㎝㎝、、4.54.5㎝㎝CC、、1.11.1㎝㎝、、2.22.2㎝㎝、、3.33.3㎝㎝、、44mm44mmDD、、11㎝㎝、、22㎝㎝、、22㎝㎝、、40mm40mm试一试试一试方法小结：判断四条线段是否成比例，首先统一四条线段的长度单位，再分别计算两条较小线段的比及两条较大线段的比，如果两个比相等，那么这四条线段成比例，如果这两个比不等，那么这四条线段不成比例.合作交流例例22、（、（11）已知）已知aa、、bb、、cc、、dd是成比例线段，是成比例线段，aa＝＝2cm2cm，，bb＝＝3cm3cm，，cc＝＝6cm6cm，求，求dd的长度；的长度；典型例题典型例题（（22）已知）已知aa＝＝2cm2cm，，bb＝＝3cm3cm，，cc＝＝6cm6cm，，请你添加一条线段，使这四条线段成比例；请你添加一条线段，使这四条线段成比例；比例的基本性质：如果a∶b=c∶d,那么____=_____;反过来,如果_____=_____,那么a∶b=c∶d或（）回顾与思考回顾与思考在a∶b=c∶d中,如果b=c,即：那么,这时,我们把b叫做a和d的比例中项.adb2adbcadbc等积式比例式acbddbba特别地：（（11）已知线段）已知线段mm、、nn、、pp、、qq的长度满足的长度满足等式等式mnmn＝＝pqpq，将它改写成比例式的形式，，将它改写成比例式的形式，错误的是错误的是()()nqpmqnmppnmqqpnmA、B、C、D、试一试试一试合作探究：观察下列式子76353010653=则5531010655310106⑴已知，==4263⑵已知442663442663则=，==⑶已知776353530776353530=则，==根据上述式子所反映的特征可得：bbaddc=bbaddc=badc=如果badc=那么::1____________1:acbdacbdabcdbdcdd因a-b同理:以即b为所===dcbaddcbba如果：那么：探究与交流._________bba)(,ba131则已知.______bba)(2.______baa)(4._____bab)(3._____bba)(251334323321473fedcbabafdbeca（1）如果，那么（2）如果，那么......acmabdnb....acmbdnaa+c+e42,bb+d+fcedf例、已知求（b+d+f≠0）思考：思考：练习1.已知(b+c):a=(a+c):b=(a+b):c=m,求m.例:已知：如图，在△ABC中，A...