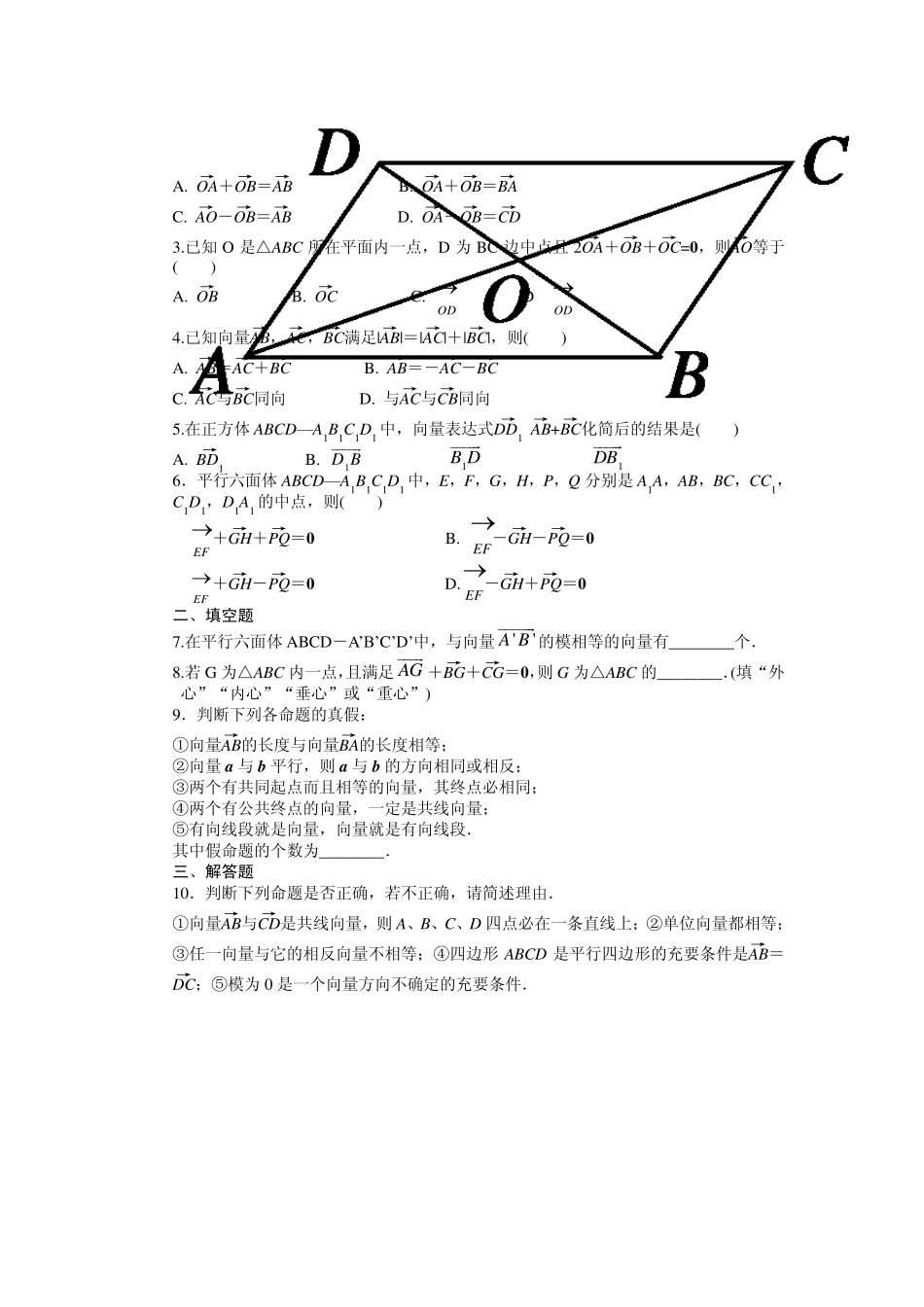
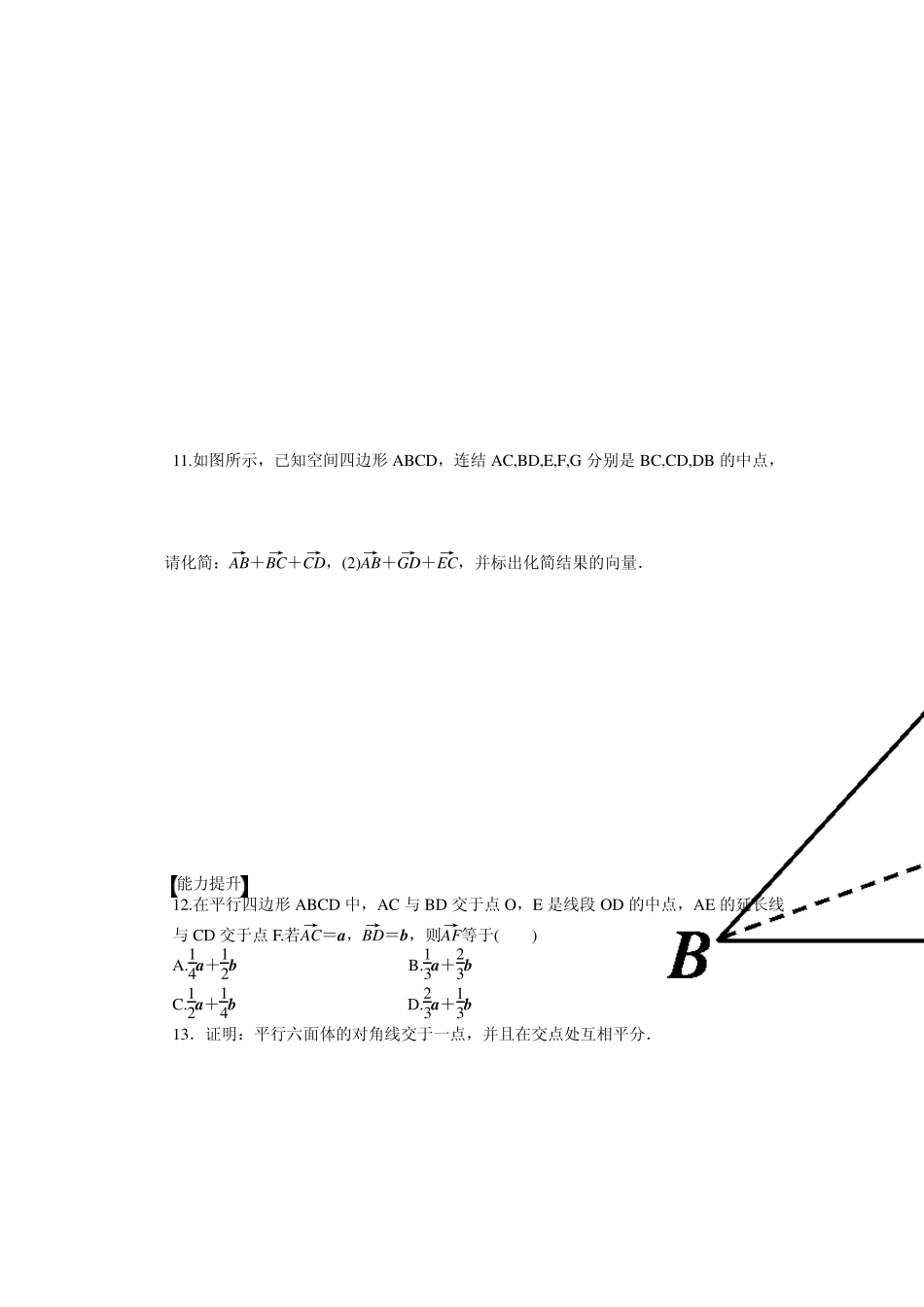
第三章 空间向量与立体几何 § 3 .1 空间向量及其运算 3 .1 .1 空间向量及其加减运算 课时目标 1.理解空间向量的概念,掌握空间向量的几何表示和字母表示. 2.掌握空间向量的加减运算及其运算律,能借助图形理解空间向量及其运算的意义. 2.几类特殊向量 (1)零向量:____________的向量叫做零向量,记为________. (2)单位向量:________的向量称为单位向量. (3)相等向量:方向________且模________的向量称为相等向量.在空间,同向且等长的有向线段表示同一向量或相等向量. (4)相反向量:与向量a 长度______而方向________的向量,称为a 的相反向量,记为________. 3.空间向量的加减法与运算律 空间向量 的加减法 类似平面向量,定义空间向量的加、减法运算(如图): OB→ =OA→ +AB→=__________;CA→=OA→ -OC→ =________. 加法运 算律 (1)交换律:a+b=________ (2)结合律:(a+b)+c=____________.; 一、选择题 1.下列命题中,假命题是( ) A. 向量AB→与BA→的长度相等 B.两个相等的向量,若起点相同,则终点也相同 C.只有零向量的模等于 0 D.共线的单位向量都相等 2.如图所示,平行四边形ABCD 的对角线的交点为O,则下列等式成立的是( ) A. OA→+OB→=AB→ B. OA→+OB→=BA→ C. AO→-OB→=AB→ D. OA→-OB→=CD→ 3.已知O 是△ABC 所在平面内一点,D 为BC 边中点且2OA→+OB→+OC→=0 ,则AO→等于( ) A. OB→ B. OC→ C. OD D.2OD 4.已知向量AB→,AC→,BC→满足|AB→|=|AC→|+|BC→|,则( ) A. AB→=AC→+BC→ B. AB→=-AC→-BC→ C. AC→与BC→同向 D. 与AC→与CB→同向 5.在正方体ABCD—A1B1C1D1 中,向量表达式DD1→-AB→+BC→化简后的结果是( ) A. BD1→ B. 1D B C.1B D D. 1DB 6.平行六面体ABCD—A1B1C1D1 中,E,F,G,H,P,Q 分别是A1A,AB,BC,CC1,C1D1,D1A1 的中点,则( ) A.EF+GH→+PQ→=0 B. EF-GH→-PQ→=0 C.EF+GH→-PQ→=0 D. EF-GH→+PQ→=0 二、填空题 7.在平行六面体ABCD-A’B’C’D’中,与向量''A B的模相等的向量有________个. 8.若G 为△ABC 内一点,且满足AG+BG→+CG→=0 ,则G 为△ABC 的________.(填“外心”“内心”“垂心”或“重心”) 9.判断下列各命题的真...