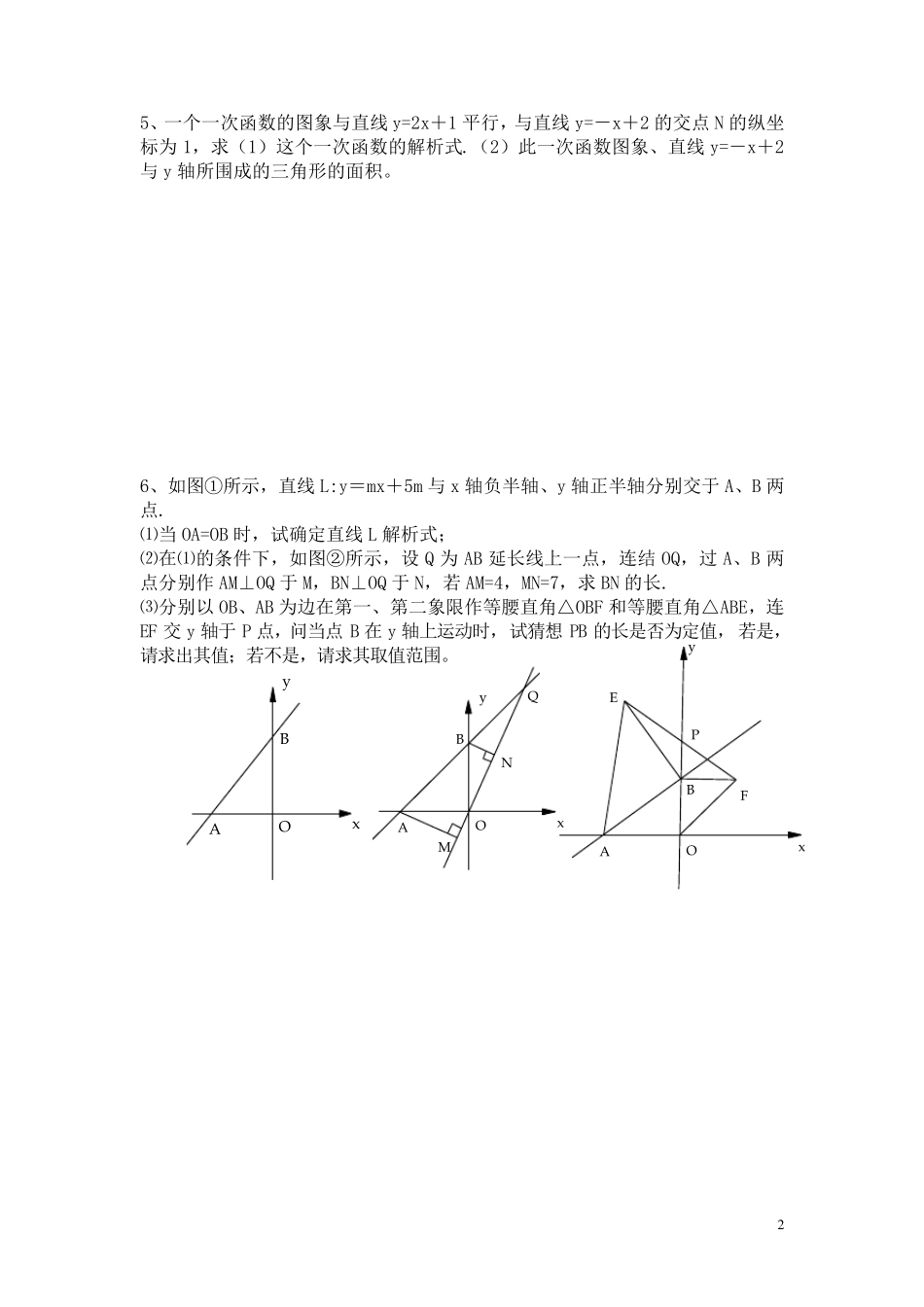
1 一次函数之数形结合典型练习 1、已知直线yaxb如图所示:试根据图象写出: (1)a ,b , (2)方程 0axb的解是 , (3)方程 1axb 的解是 。 .2、函数y=ax+b 与y=bx+a 的图象在同一坐标系内的大致位置正确的是( ) A. B. C. D. 3、把直线121xy向上平移21 个单位,可得到函数__________________.接着向右平移3 个单位,可得函数 。直线121xy关于y 轴对称的直线解析式为 ,关于x 轴对称的直线解析式为 ,关于原点对称的直线解析式为 。 4、如右图,A、B 分别是x 轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA 交y 轴于点C(0,2),直线PB 交y 轴于点D,S△AOP=6。 (1)求点A 的坐标及 P 的值。 (2)若 S△BOP=S△DOP,求直线BD 的函数解析式。 yx112y=ax+bODBCAOPxy 2 5、一个一次函数的图象与直线y=2x+1 平行,与直线y=-x+2 的交点N 的纵坐标为1,求(1)这个一次函数的解析式.(2)此一次函数图象、直线y=-x+2与y 轴所围成的三角形的面积。 6、如图①所示,直线L:y=mx+5m 与x 轴负半轴、y 轴正半轴分别交于A、B 两点. ⑴当OA=OB 时,试确定直线L 解析式; ⑵在⑴的条件下,如图②所示,设Q 为AB 延长线上一点,连结OQ,过A、B 两点分别作AM⊥OQ 于M,BN⊥OQ 于N,若 AM=4,MN=7,求BN 的长. ⑶分别以 OB、AB 为边在第一、第二象限作等腰直角△OBF 和等腰直角△ABE,连EF 交y 轴于P 点,问当点B 在y 轴上运动时,试猜想 PB 的长是否为定值,若是,请求出其值;若不是,请求其取值范围。 QNMyxOBAFPEyxOBAyxOBA 3 7、如图1,已知直线y =2x +2 与y 轴、x 轴分别交于A、B 两点,以B 为直角顶点在第二象限作等腰Rt△ABC. (1)求点C 的坐标,并求出直线AC 的关系式. (2)如图2,直线CB 交y 轴于E,在直线CB 上取一点D,连接 AD,若 AD=AC,求证:BE=DE. (3)如图3,在(1)的条件下,直线AC 交x 轴于M,P(25,k)是线段 BC 上一点,在线段 BM 上是否存在一点N,使直线PN 平分△BCM 的面积?若存在,请求出点N 的坐标;若不存在,请说明理由. yxOABCDE图2 yxOABC图1 yxABCOPM图3 4 8、如图,直线y=x+1 交x轴于点A,交y轴于点C,OB=3OA,M 在直线AC 上,AC=CM. (1)求直线BM 的解析式; (2)如图点N 在MB 的延长线上,BN=CM,连CN 交x轴于点P,求点P 的坐标; (3)...