十字相乘法因式分解

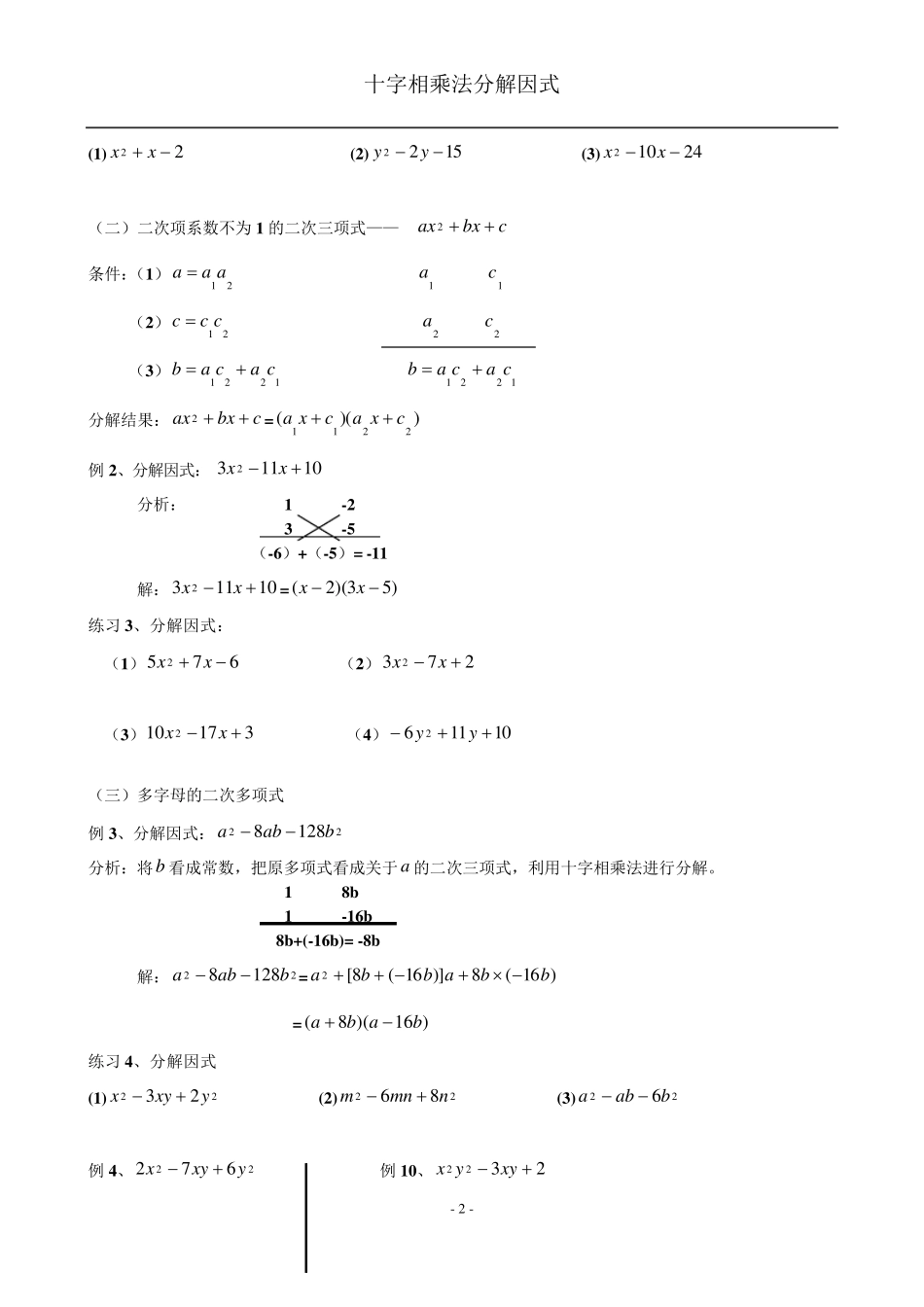
十字相乘法分解因式 - 1 - 十字相乘法分解因式 (1)对于二次项系数为1 的二次三项式))(()(2bxaxabxbax 方法的特征是“拆常数项，凑一次项” 当常数项为正数时，把它分解为两个同号因数的积，因式的符号与一次项系数的符号相同； 当常数项为负数时，把它分解为两个异号因数的积，其中绝对值较大的因数的符号与一次项系数的符号相同． (2)对于二次项系数不是1 的二次三项式 cbxax2))(()(2211211221221cxacxaccxcacaxaa 它的特征是“拆两头，凑中间” 当二次项系数为负数时，先提出负号，使二次项系数为正数，然后再看常数项； 常数项为正数时，应分解为两同号因数，它们的符号与一次项系数的符号相同； 常数项为负数时，应将它分解为两异号因数，使十字连线上两数之积绝对值较大的一组与一次项系数的符号相同 注意：用十字相乘法分解因式，还要注意避免以下两种错误出现：一是没有认真地验证交叉相乘的两个积的和是否等于一次项系数；二是由十字相乘写出的因式漏写字母． 二、典型例题 例5、分解因式：652 xx 分析：将6 分成两个数相乘，且这两个数的和要等于5。 由于6=2×3=(-2)×(-3)=1×6=(-1)×(-6)，从中可以发现只有2×3 的分解适合，即 2+3=5。 1 2 解：652 xx=32)32(2xx 1 3 =)3)(2(xx 1×2+1×3=5 用此方法进行分解的关键：将常数项分解成两个因数的积，且这两个因数的代数和要等于一次项的系数。 例1、分解因式：672 xx 解：原式=)6)(1()]6()1[(2xx 1 -1 =)6)(1(xx 1 -6 （-1）+（-6）= -7 练习 1、分解因式 (1)24142xx (2)36152aa (3)542 xx 练习 2、分解因式 十字相乘法分解因式 - 2 - (1)22 xx (2)1522yy (3)24102xx （二）二次项系数不为1 的二次三项式—— cbxax2 条件：（1）21aaa  1a 1c （2）21ccc  2a 2c （3）1221cacab 1221cacab 分解结果：cbxax2=))((2211cxacxa 例 2、分解因式：101132xx 分析： 1 -2 3 -5 （-6）+（-5）= -11 解：101132xx=)53)(2(xx 练习 3、分解因式： （1）6752 xx （2）2732 xx （3）317102xx （4）101162yy （三）多字母的二次多项式 例 3、分解因式：221288baba 分析：将b 看成常数，把原多项式看成关于a 的二次三项式，利用十字相...