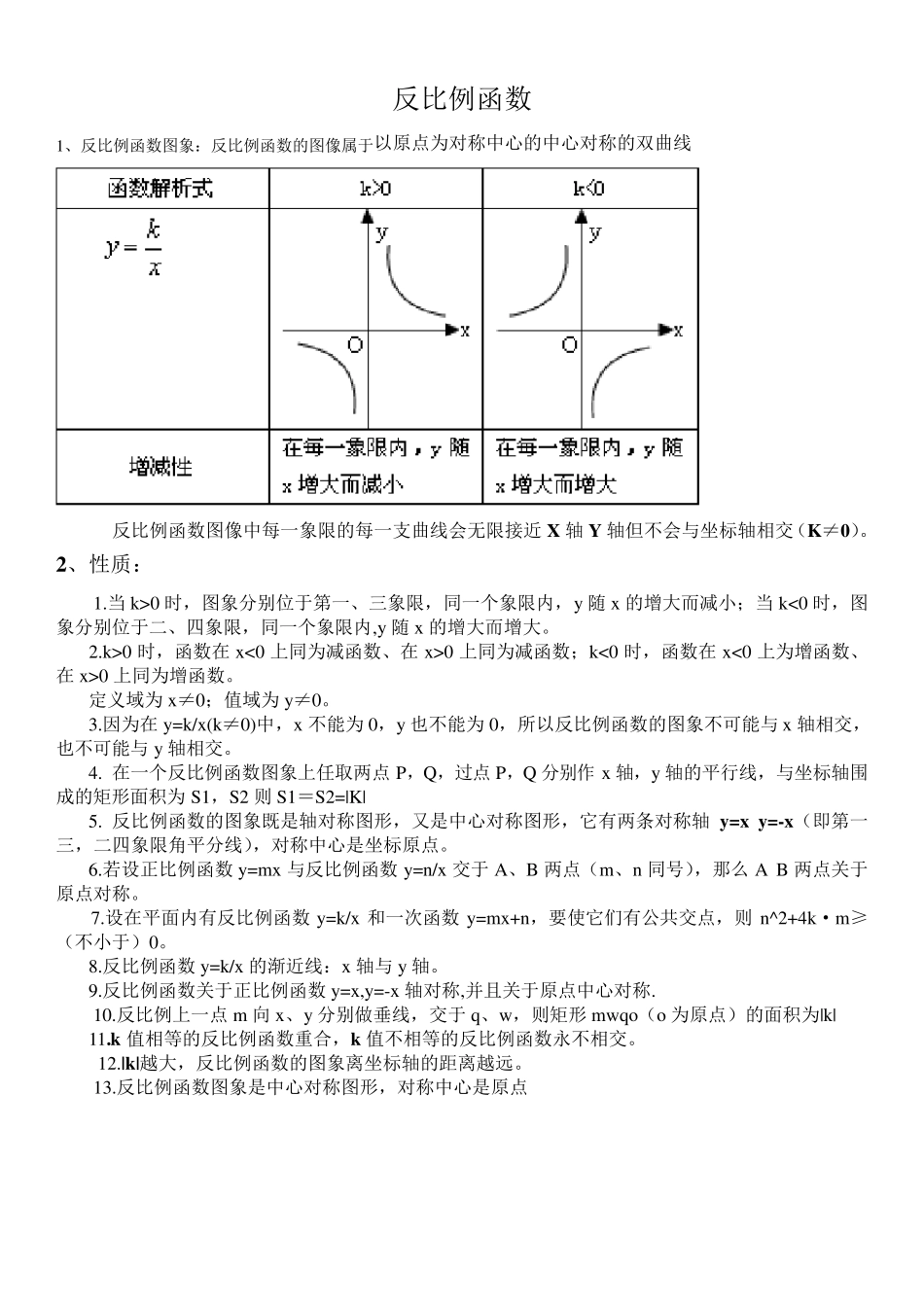
反比例函数 1、反比例函数图象:反比例函数的图像属于以原点为对称中心的中心对称的双曲线 反比例函数图像中每一象限的每一支曲线会无限接近X 轴Y 轴但不会与坐标轴相交(K≠0)。 2、性质: 1.当k>0 时,图象分别位于第一、三象限,同一个象限内,y 随x 的增大而减小;当k<0 时,图象分别位于二、四象限,同一个象限内,y 随x 的增大而增大。 2.k>0 时,函数在x<0 上同为减函数、在x>0 上同为减函数;k<0 时,函数在x<0 上为增函数、在x>0 上同为增函数。 定义域为x≠0;值域为y≠0。 3.因为在y=k/x(k≠0)中,x 不能为0,y 也不能为0,所以反比例函数的图象不可能与x 轴相交,也不可能与y 轴相交。 4. 在一个反比例函数图象上任取两点P,Q,过点P,Q 分别作x 轴,y 轴的平行线,与坐标轴围成的矩形面积为S1,S2 则S1=S2=|K| 5. 反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴 y=x y=-x(即第一三,二四象限角平分线),对称中心是坐标原点。 6.若设正比例函数y=mx 与反比例函数y=n/x 交于A、B 两点(m、n 同号),那么A B 两点关于原点对称。 7.设在平面内有反比例函数y=k/x 和一次函数y=mx+n,要使它们有公共交点,则n^2+4k·m≥(不小于)0。 8.反比例函数y=k/x 的渐近线:x 轴与y 轴。 9.反比例函数关于正比例函数y=x,y=-x 轴对称,并且关于原点中心对称. 10.反比例上一点m 向 x、y 分别做垂线,交于q、w,则矩形mwqo(o 为原点)的面积为|k| 11.k 值相等的反比例函数重合,k 值不相等的反比例函数永不相交。 12.|k|越大,反比例函数的图象离坐标轴的距离越远。 13.反比例函数图象是中心对称图形,对称中心是原点 一次函数 (一)函数 1 、确定函数定义域的方法: (1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零; (3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零; (5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。 (二)一次函数 1、一次函数的定义 一般地,形如ykxb(k ,b 是常数,且0k )的函数,叫做一次函数,其中x 是自变量。当0b 时,一次函数ykx,又叫做正比例函数。 ⑴一次函数的解析式的形式是ykxb,要判断一个函数是否是一次函数,就是判断是否能化成以上形式. ⑵当0b ,0k 时,ykx...