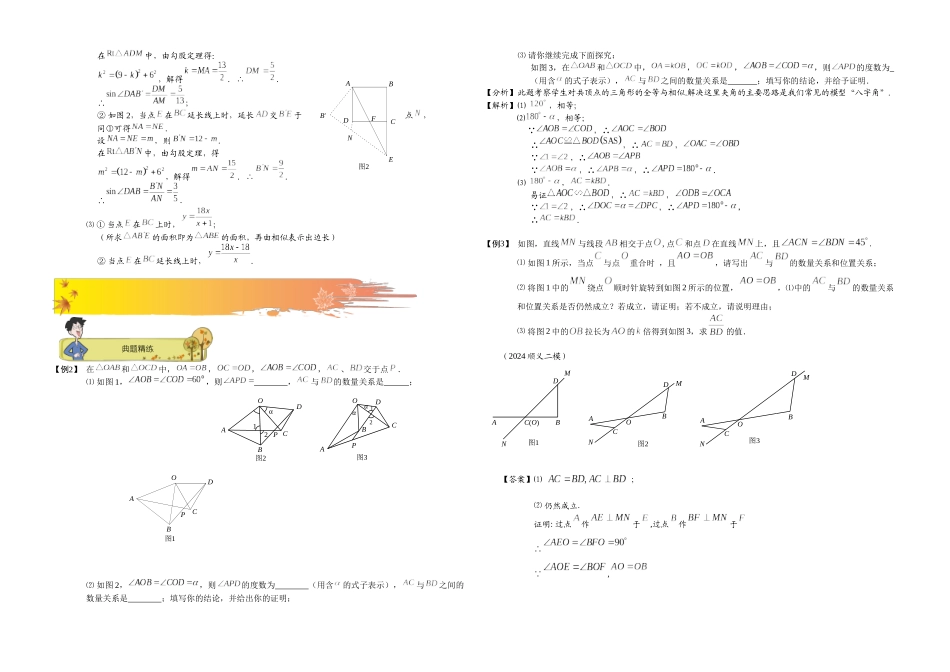
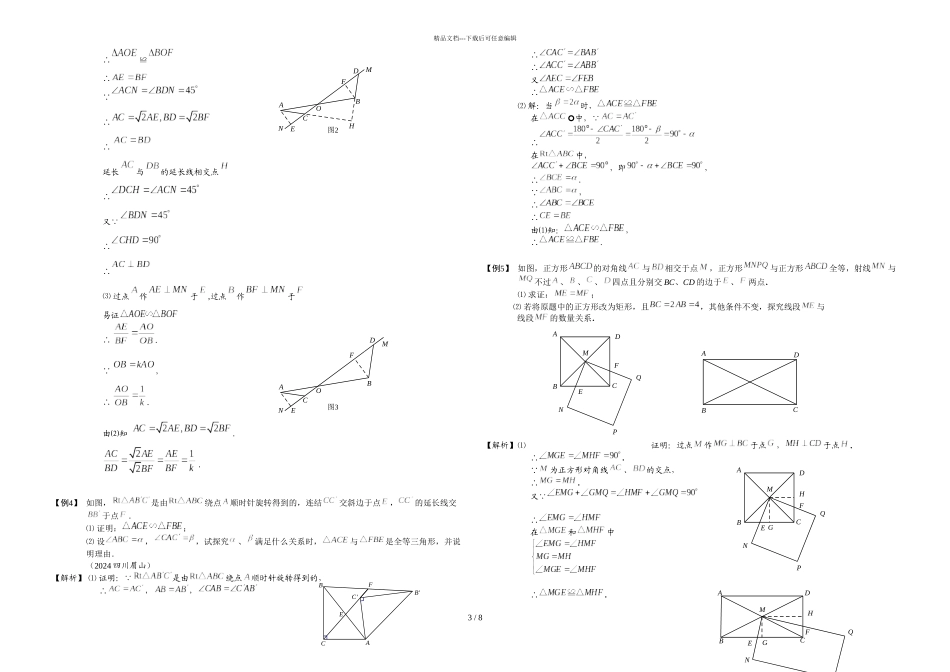
8全等到相似的转化满分晋级阶梯三角形 17 级解直角三角形三角形 16 级全等到相似的转化三角形 15 级垂直模型中的相似及变形秋季班第九讲秋季班第八讲秋季班第七讲漫画释义知识互联网典题精练精品文档---下载后可任意编辑 克隆机 VS 放大机 【例1】 已知正方形的边长为,点是射线上的一个动点,连接交射线于点,将沿直线翻折,点落在点处. ⑴ 当时,______, ⑵ 当时,求的值; ⑶ 当时(点与点不重合),请写出翻折后与正方形公共部分的面积与的关系式,(只要写出结论,不要解题过程).【解析】 ⑴ 6 ; ⑵ ① 如图 1,当点在上时,延长交于点, ,∴,∴. ,∴. ,∴.又,∴.∴.设,则,.1 / 8题型一:全等到相似的转化(对称型)图1B′MFEDCBADCBAα图2DP CABO2121ααPBODC图3A典题精练在中,由勾股定理得:,解得.∴.∴; ② 如图 2,当点在延长线上时,延长交于点,同①可得.设,则.在中,由勾股定理,得,解得.∴.∴. ⑶ ① 当点在上时,; (所求的面积即为的面积,再由相似表示出边长) ② 当点在延长线上时,. 【例2】 在和中,,,,、交于点. ⑴ 如图 1,,则 ,与的数量关系是 ; ⑵ 如图 2,,则的度数为 (用含的式子表示),与之间的数量关系是 ;填写你的结论,并给出你的证明; ⑶ 请你继续完成下面探究:如图 3,在和中,,,,则的度数为 (用含的式子表示),与之间的数量关系是 ;填写你的结论,并给予证明.【分析】此题考察学生对共顶点的三角形的全等与相似.解决这里夹角的主要思路是我们常见的模型“八字角”.【解析】⑴ ,相等;⑵,相等; ,∴∴,∴, ,∴ ,∴,∴.⑶ ,.易证,∴, ,∴,∴,∴.【例3】 如图,直线与线段相交于点, 点和点在直线上,且. ⑴ 如图 1 所示,当点与点重合时 ,且,请写出与的数量关系和位置关系; ⑵ 将图 1 中的绕点顺时针旋转到如图 2 所示的位置,,⑴中的与的数量关系和位置关系是否仍然成立?若成立,请证明;若不成立,请说明理由; ⑶ 将图 2 中的拉长为的倍得到如图 3,求的值.(2024 顺义二模)【答案】⑴ ; ⑵ 仍然成立.证明: 过点作于,过点作于∴ ,题型二:全等到相似的转化(旋转型)图2B′NFEDCBA图1PODCBA图1NMDBC(O)A图2DMNOCBAABCONMD图3FECBAB'C'HGNPQMFEDCBAMHGFQPNEDCBANPQMFEDCBA精品文档---下载后可任意编辑∴≌∴ ∴ ∴延长与的延长线相交点...