正弦函数和余弦函数图像与性质

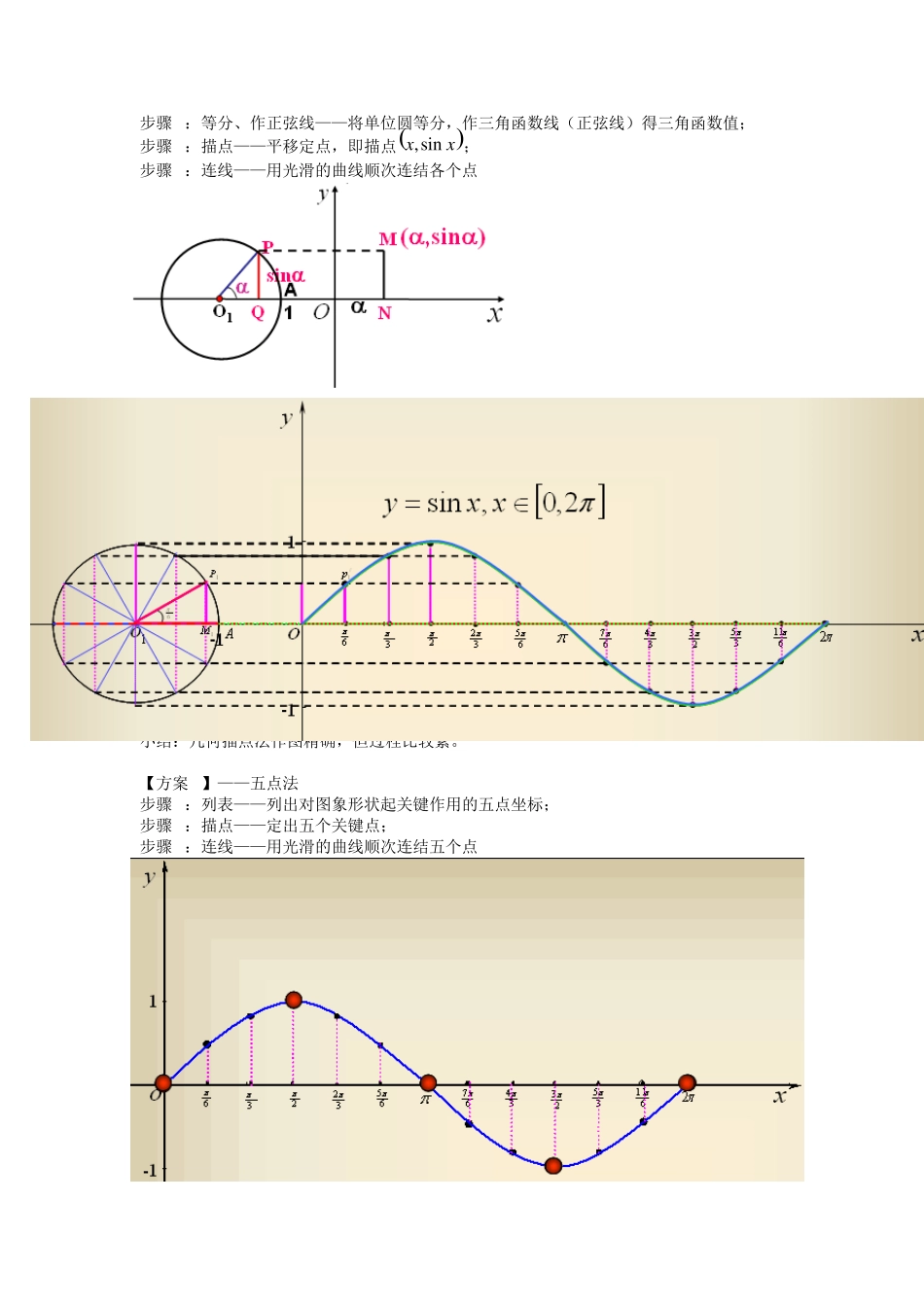
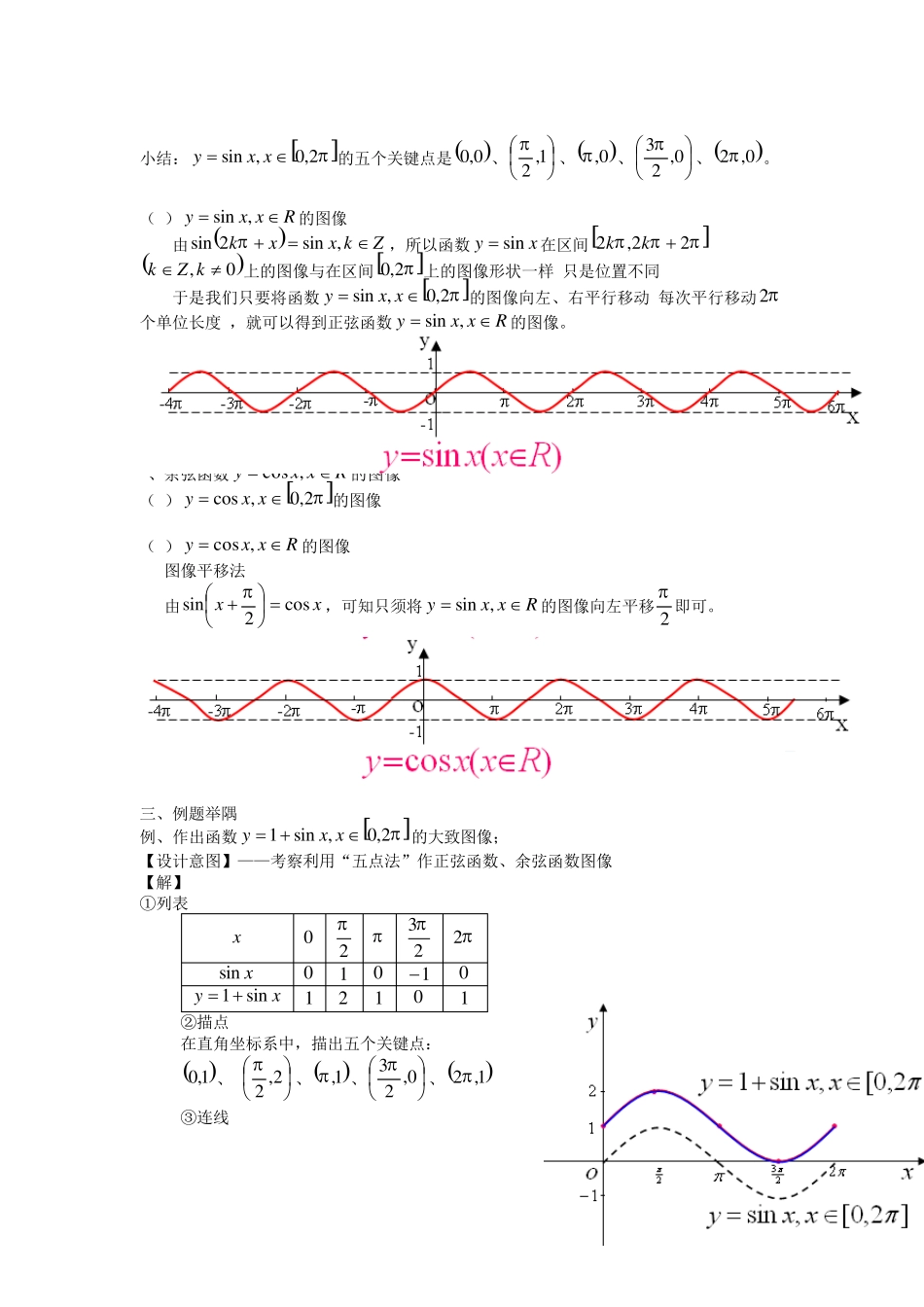
6.1 正弦函数和余弦函数的图像与性质 一、复习引入 1、复习 （1）函数的概念 在某个变化过程中有两个变量x 、y ，若对于x 在某个实数集合D 内的每一个确定的值，按照某个对应法则f ，y 都有唯一确定的实数值与它对应，则y 就是x 的函数，记作 xfy ，Dx 。 （2）三角函数线 设任意角 的顶点在原点O ，始边与x 轴的非负半轴重合，终边与单位圆相交于点( , )P x y ，过P 作x 轴的垂线，垂足为M ；过点(1,0)A作单位圆的切线，设它与角 的终边（当 在第一、四象限角时）或其反向延长线（当 为第二、三象限角时）相交于T . 规定：当OM 与x 轴同向时为正值，当OM 与x 轴反向时为负值； 当MP 与y 轴同向时为正值，当MP 与y 轴反向时为负值； 当AT 与y 轴同向时为正值，当AT 与y 轴反向时为负值； 根据上面规定，则,OMx MPy, 由正弦、余弦、正切三角比的定义有： sin1yyyMPr ； cos1xxxOMr ； tanyMPATATxOMOA ； 这几条与单位圆有关的有向线段,,MP OM AT 叫做角 的正弦线、余弦线、正切线。 二、讲授新课 【问题驱动1】——结合我们刚学过的三角比，就以正弦(或余弦)为例，对于每一个给定的角和它的正弦值(或余弦值)之间是否也存在一种函数关系？若存在，请对这种函数关系下一个定义；若不存在，请说明理由． 1、正弦函数、余弦函数的定义 （1）正弦函数：Rxxy,sin； （2）余弦函数：Rxxy,cos 【问题驱动2】——如何作出正弦函数Rxxy,sin、余弦函数Rxxy,cos的函数图象？ 2、正弦函数Rxxy,sin的图像 （1）2,0,sinxxy的图像 【方案 1】——几何描点法 步骤1：等分、作正弦线——将单位圆等分，作三角函数线（正弦线）得三角函数值； 步骤2：描点——平移定点，即描点xx sin,； 步骤3：连线——用光滑的曲线顺次连结各个点 小结：几何描点法作图精确，但过程比较繁。 【方案 2】——五点法 步骤1：列表——列出对图象形状起关键作用的五点坐标； 步骤2：描点——定出五个关键点； 步骤3：连线——用光滑的曲线顺次连结五个点 小结：2,0,sinxxy的五个关键点是0,0、1,2、0,、 0,23、0,2。 （2）Rxxy,sin的图像 由Zkxxk,sin2sin，所以函数 xysin在区间22,2kk 0,kZk上的图像与在...