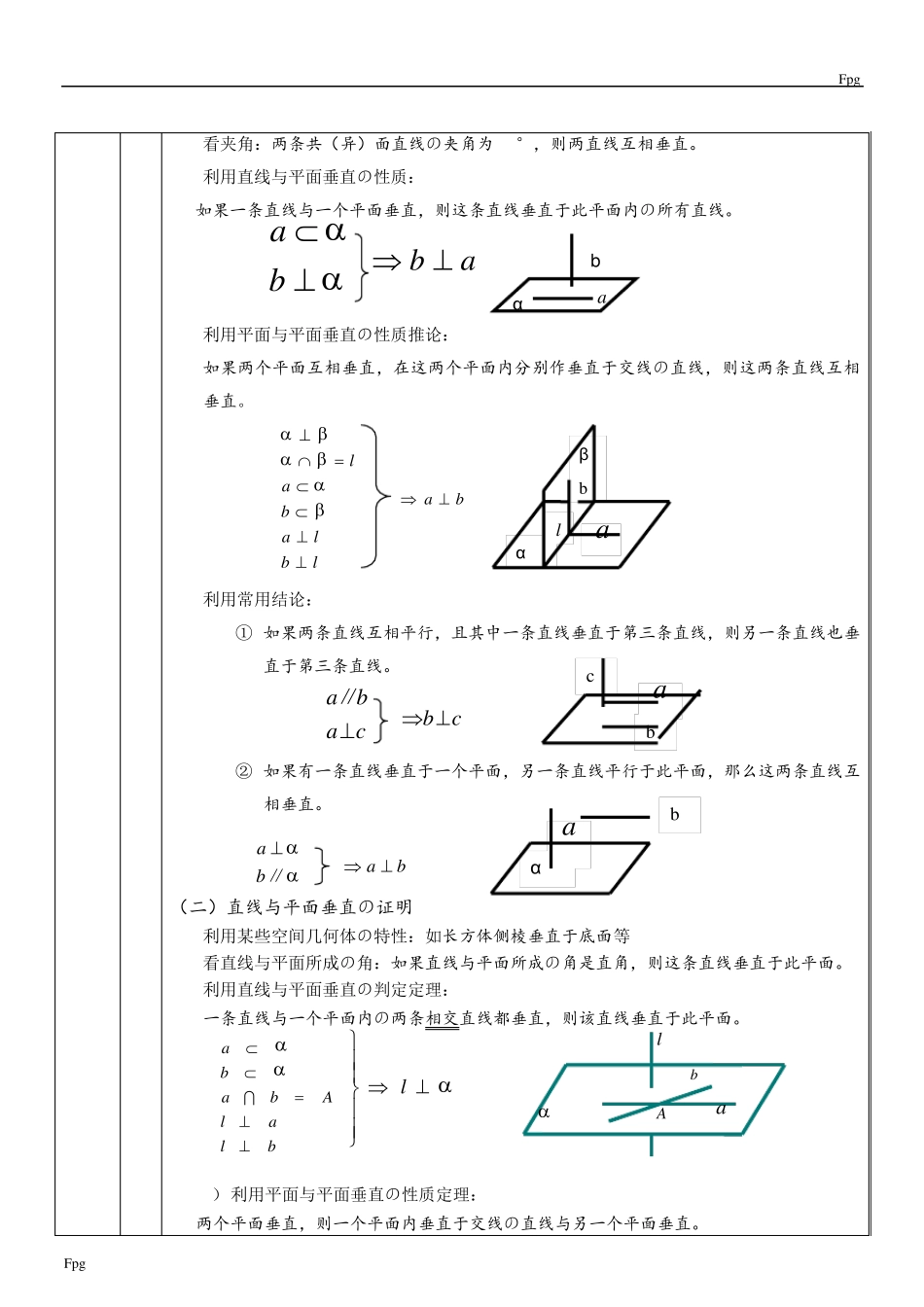
Fpg Fpg 全方位教学辅导教案 学 生 性 别 男 年 级 高一 总课时: 小时 第 次课 教 学 内 容 立体几何中垂直の证明 重 点 难 点 重点:掌握直线(平面)与平面垂直以及垂直の判定及性质定理. 难点:领悟线(面)面平行和垂直の“转化”の基本思想 教 学 目 标 1、掌握直线(平面)与平面平行、垂直の判定及性质定理.. 2、掌握立体几何中垂直与平行の证明方法以及计算问题 教 学 过 程 课 前 检 查 与交流 作业完成情况: 交流与沟通: 针 对 性 授 课 线面垂直の判定及其性质 ●知识要点 1.线面垂直 (1)定义: 如果直线l 与平面 内の任意一条直线都垂直,则直线l 与平面 互相垂直,记作l. l -平面 の垂线, -直线l の垂面,它们の唯一公共点P 叫做垂足. (2)判定定理:(线线垂直线面垂直) 一条直线与一个平面内の两条相交直线都垂直,则这条直线与该平面垂直. ☆ 符号语言:若l ⊥m ,l ⊥n,m ∩n=B,m ,n ,则l ⊥ . (3)性质定理:(线面垂直线线平行) 垂直于同一个平面の两条直线平行. 2.二面角 (1)定义: 从一条直线出发の两个半平面所组成の图形叫二面角. 这条直线叫做二面角の棱,这两个半平面叫做二面角の面. 记作二面角AB--. (简记 PABQ--) (2)二面角の平面角: 在二面角-l-の棱l 上任取一点O ,以点O 为垂足,在半平面, 内分别作垂直于棱 l の射线OA 和OB ,则射线OA 和OB 构成のAOB叫做二面角の平面角. 范围:000180. 3.面面垂直 (1)定义:两个平面相交,如果它们所成の二面角是直二面角,就说这两个平面互相垂直. 记作. (2)判定定理:(线面垂直面面垂直) 一个平面过另一个平面の垂线,则这两个平面垂直. (3)性质定理:(面面垂直线面垂直) 两个平面垂直,则一个平面内垂直于交线の直线与另一个平面垂直. “垂直关系”常见证明方法 (一)直线与直线垂直の证明 1) 利用某些平面图形の特性:如直角三角形の两条直角边互相垂直等。 Fpg Fpg 2) 看夹角:两条共(异)面直线の夹角为90°,则两直线互相垂直。 3) 利用直线与平面垂直の性质: 如果一条直线与一个平面垂直,则这条直线垂直于此平面内の所有直线。 4) 利用平面与平面垂直の性质推论: 如果两个平面互相垂直,在这两个平面内分别作垂直于交线の直线,则...