立体几何大题

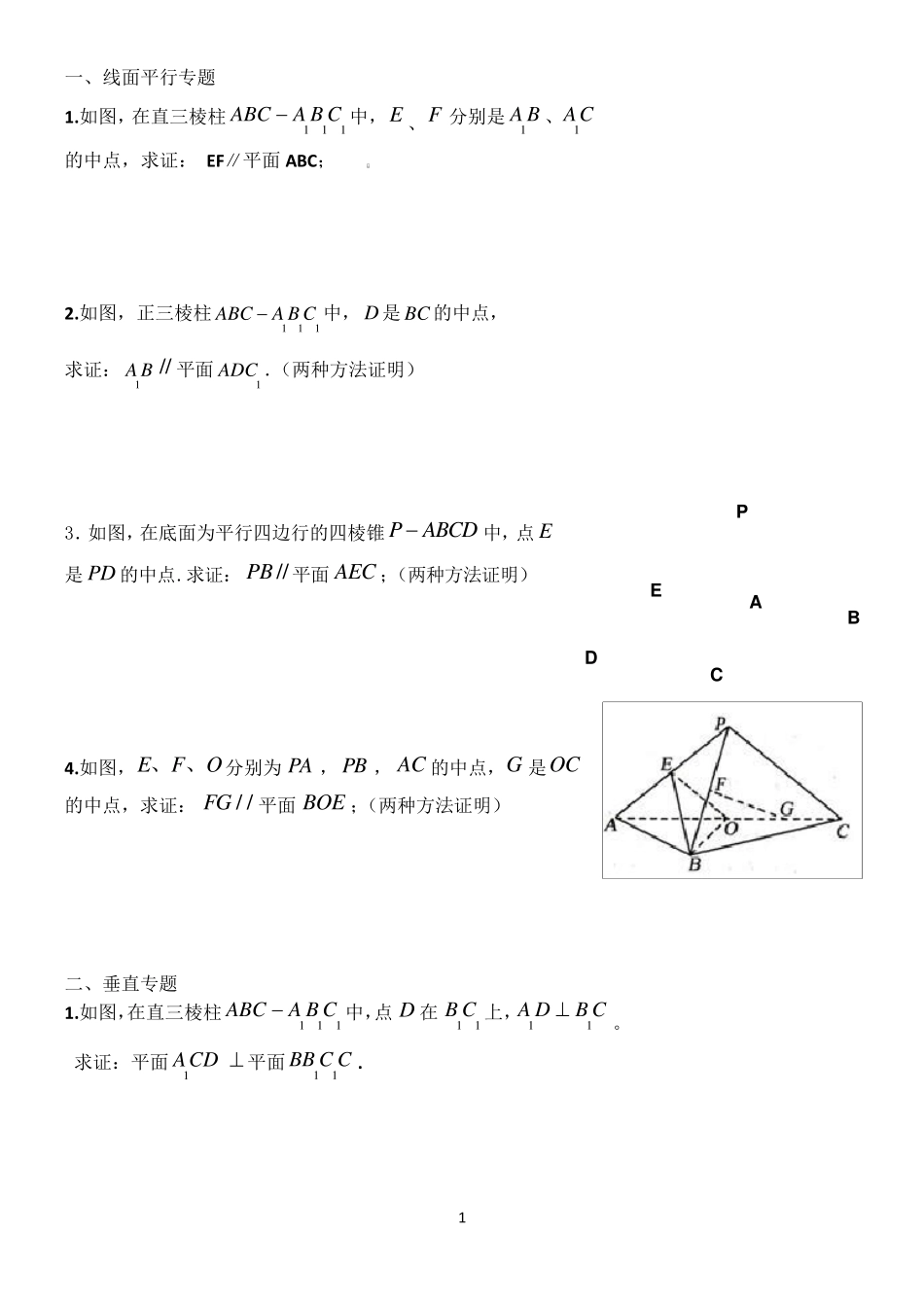
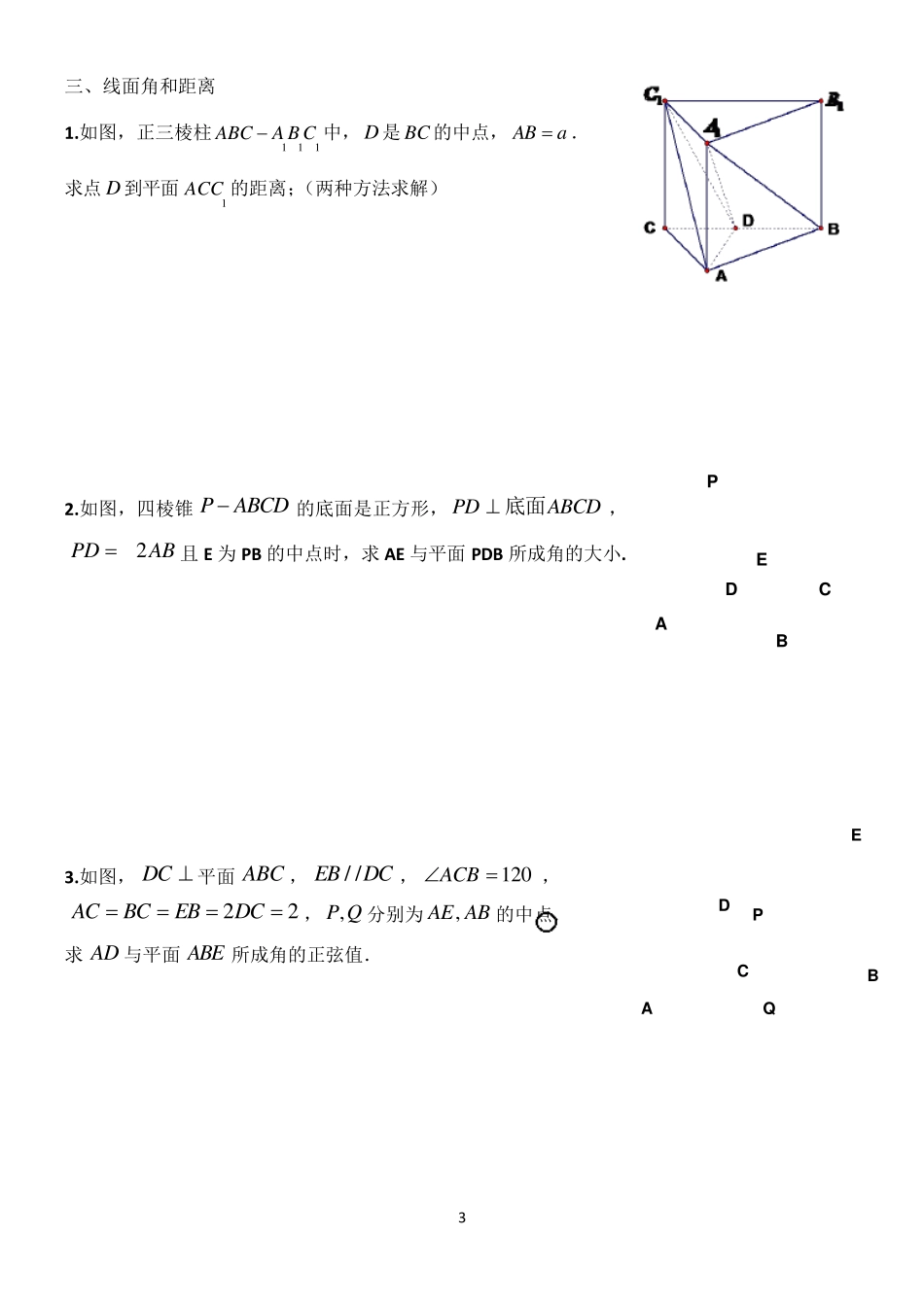
1 一、线面平行专题 1.如图，在直三棱柱中，、分别是、的中点，求证： EF∥平面ABC； 2.如图，正三棱柱111ABCA B C中，D 是BC 的中点， 求证：1A B // 平面1ADC ．（两种方法证明） 3．如图，在底面为平行四边行的四棱锥 PABCD中，点E是PD 的中点.求证：//PB平面AEC ；（两种方法证明） 4.如图，EFO、、分别为，，的中点，是的中点，求证： 平面；（两种方法证明） 二、垂直专题 1.如图，在直三棱柱中，点在上，。 求证：平面1ACD平面. 111ABCA B CEF1A B1ACPAPBACGOC/ /FGBOE111ABCA B CD11B C11A DB C11BB C CPABCDE2 2.如图，正三棱柱111ABCA B C中，D 是BC 的中点，ABa． 求证：直线111A DB C； 3.如图，四棱锥的底面是正方形，，点E 在棱PB 上. 求证：平面； 4.如图，直三棱柱中，AB=1，，∠ABC=60.求证：； 5. 直三棱柱111ABCA B C中，90BAC，12ABACAA，MN、分别是1BCCC、的中点，求证：1B M  平面AMN ； 6.如图，在三棱锥中，⊿是等边三角形， ∠PAC=∠PBC=90º。 求证：AB⊥ PC PABCDPDABCD 底面AECPDB 平面111ABCA B C13ACAA01ABACPABCPABPBACDEPBCA3 三、线面角和距离 1.如图，正三棱柱111ABCA B C中， D 是 BC 的中点， ABa． 求点 D 到平面1ACC 的距离；（两种方法求解） 2.如图，四棱锥的底面是正方形，，且 E 为 PB 的中点时，求 AE 与平面 PDB 所成角的大小. 3.如图，平面，，， ，分别为的中点． 求与平面所成角的正弦值． PABCDPDABCD 底面2PDABDC ABC/ /EBDC1 2 0ACB22ACBCEBDC,P Q,AE ABADABEPBACDEACDBEQP4 4.如图3，在正三棱柱中，AB=4, ,点D 是BC的中点，点E在AC 上，且DEE. （Ⅰ）证明：平面平面; （Ⅱ）求直线 AD 和平面所成角的正弦值。（两种方法求解） 5.如图，在四棱锥PABCD中，侧面 PAD 底面 ABCD ， 侧棱2PAPD,底面 ABCD 为直角梯形，其中BCAD∥， ABAD，222ADABBC. (Ⅰ) 求异面直线 PB 与CD 所成角；(Ⅱ) 求 PC 与平面 ABCD 所成的角； (Ⅲ)求点A到平面PCD的距离. 6.如图，在正三棱柱中，12ABAA，D 是的中点，点E在上，且。（1）证明平面平面； （2）求直线和平面 ABC所成的角。 111ABCA B C17AA 1A1A DE 11ACC A1A DE111ABCA B C11A B11ACDEAEADE 11A...