正态分布指数分布对数正态分布和威布尔分布函数和在工程分析中的应用

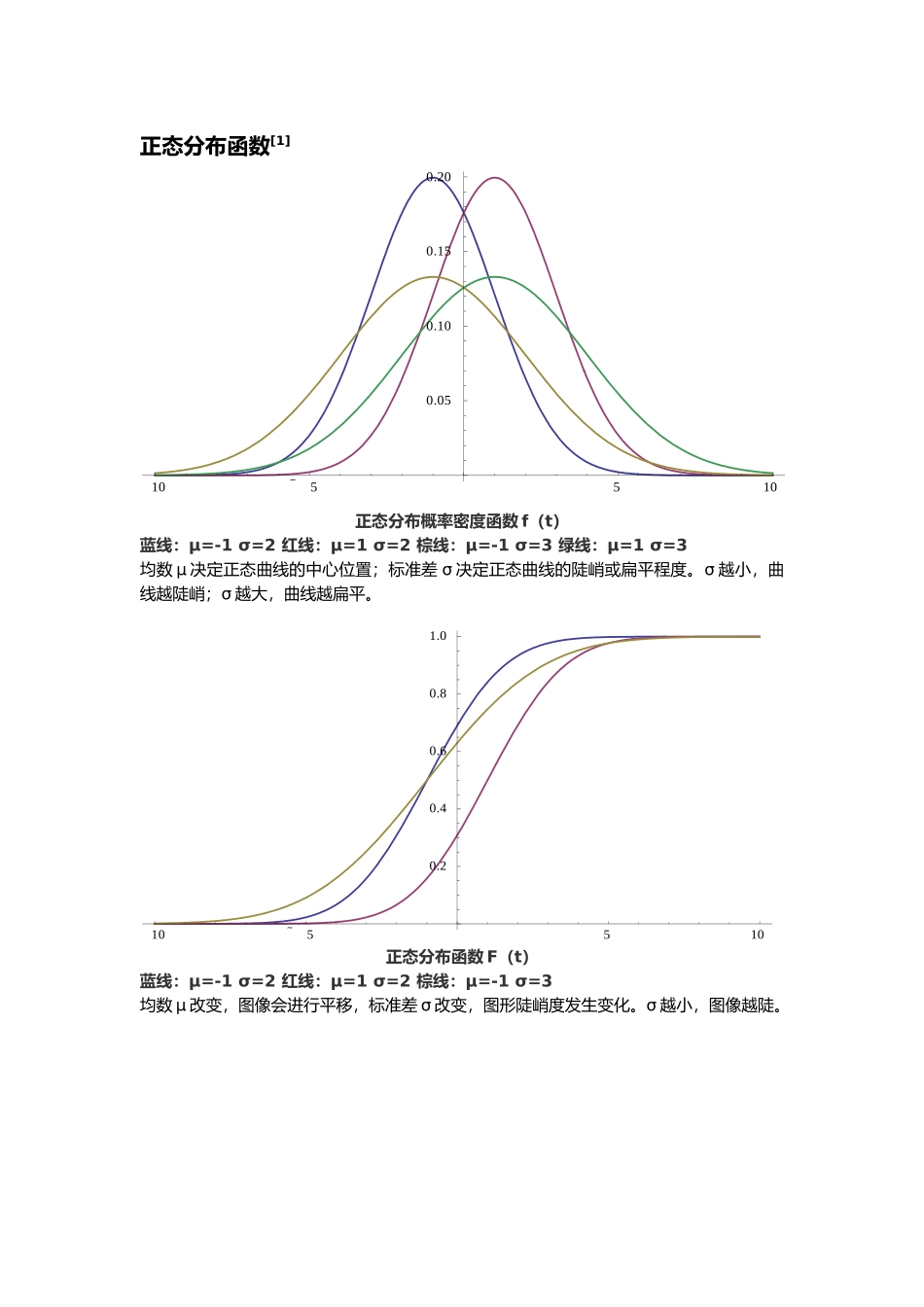
正态分布、指数分布、对数正态分布和威布尔分布函数与其在工程分析中的应用071330225 洋洋目录正态分布函数 3正态分布应用领域 4正态分布案例分析 5指数分布函数 5指数分布的应用领域 6指数分布案例分析 7对数正态分布函数 7对数正态分布的应用领域 9对数正态分布案例分析 9威布尔分布函数 10威布尔分布的应用领域 16威布尔分布案例分析 16附录 18参考文献 21正态分布函数[1]1055100.050.100.150.20正态分布概率密度函数 f（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3 绿线：μ=1 σ=3均数 μ 决定正态曲线的中心位置；标准差 σ 决定正态曲线的陡峭或扁平程度。σ 越小，曲线越陡峭；σ 越大，曲线越扁平。1055100.20.40.60.81.0正态分布函数 F（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3均数 μ 改变，图像会进行平移，标准差 σ 改变，图形陡峭度发生变化。σ 越小，图像越陡。1055100.20.40.60.81.0正态分布可靠度函数 R（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3均数 μ 改变，图像会进行平移，标准差 σ 改变，图形陡峭度发生变化。σ 越小，图像越陡。1055100.51.01.52.02.5正态分布失效率函数 λ（t）蓝线：μ=-1 σ=2 红线：μ=1 σ=2 棕线：μ=-1 σ=3均数 μ 改变，图像会进行平移，标准差 σ 改变，图形陡峭度发生变化。σ 越小，图像越陡。正态分布应用领域[1]正态分布是一种最常见的连续型随机变量的分布,它在概率论和数理统计中无论在理论讨论还是实际应用上都占有头等重要的地位,这是因为它在误差理论、无线电噪声理论、自动控制、产品检验、质量控制、质量管理等领域都有广泛应用.数理统计中许多重要问题的解决都是以正态分布为基础的.某些医学现象，如同质群体的身高、红细胞数、血红蛋白量、胆固醇等，以与实验中的随机误差，呈现为正态或近似正态分布；有些资料虽为偏态分布，但经数据变换后可成为正态或近似正态分布，故可按正态分布规律处理。正态分布案例分析[1]例 1.10 某 地 1993 年 抽 样 调 查 了 100 名 18 岁 男 大 学 生 身 高 （ cm ） ， 其 均 数=172.70cm，标准差 s=4.01cm，①估量该地 18 岁男大学生身高在 168cm 以下者占该地 18 岁男大学生总数的百分数；②分别求 X+-1s、X+-1.96s、X+-2.58s 围 18 岁男大学生占该地 18 岁男大学生总数的实...