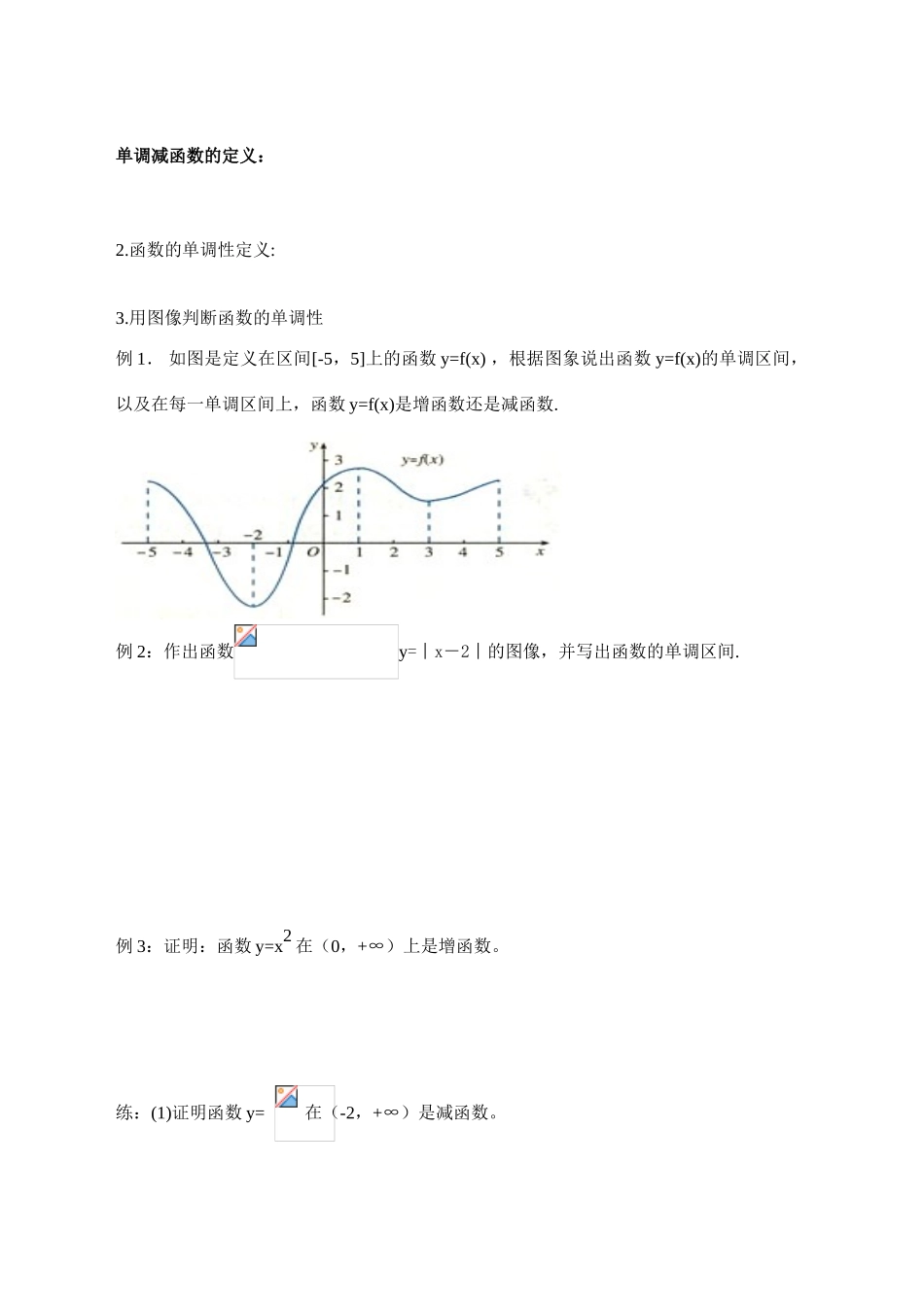
函数的简单性质:单调性(一)主备人:张丽华【教学目标】1、使学生理解增减函数的概念,并会用定义判断函数的单调性; 2、会用定义法,直接法,图象法判断函数的单调性; 3、培养学生利用数学概念进行推理的判断能力。【教学重难点】1、函数单调性的概念2、函数单调性的判断与证明情景:回想一下本章开头时的气温变化图1、问题:说出气温在哪些时段内是升高的,怎样用数学语言刻画“随时间的增大气温逐步升高”这一特征.2.画出下列函数的图像,观察其变化规律(1)f(x)=x ① 从左至右图像上升还是下降?② 在区间_____上,随着 x 的增大,相应的 f(x) 值随着____(2)f(x)=x2 ① 在区间_____上, f(x)的值随着 x 的增大而 ________ . 在区间_____上, f(x)的值随着 x 的增大而 ________ .如何用数学的语言来准确地表述函数的单调性呢?例如,怎样表述当 x 的值在区间(0,)上增大时,函数 y 的值也增大?单调增函数的定义: 单调减函数的定义: 2.函数的单调性定义: 3.用图像判断函数的单调性例 1. 如图是定义在区间[-5,5]上的函数 y=f(x) ,根据图象说出函数 y=f(x)的单调区间,以及在每一单调区间上,函数 y=f(x)是增函数还是减函数. 例 2:作出函数y=︱x-2︱的图像,并写出函数的单调区间.例 3:证明:函数 y=x2 在(0,+∞)上是增函数。练:(1)证明函数 y= 在(-2,+∞)是减函数。(2)证明函数 在 上是增函数总结:判断函数单调性的方法步骤 利用定义证明函数 f(x)在给定的区间 D 上的单调性的一般步骤: