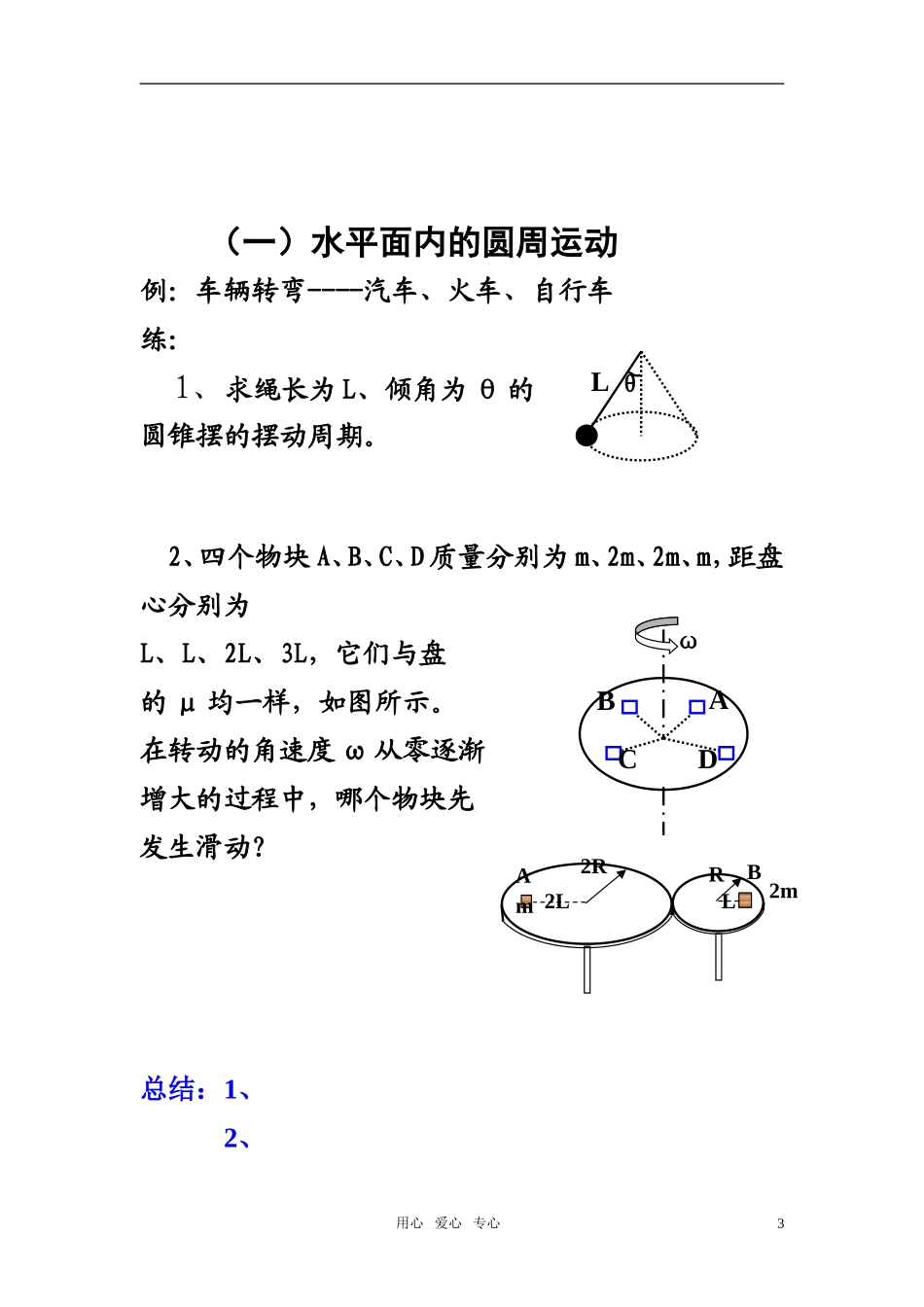
圆周运动中的动力学问题教学目标:(知识与技能)知识巩固 提高能力方法思路:提炼方法重难点:受力分析教学流程------向心力公式:F=ma= mrω2 = mv2/r = mωv --- 瞬时对应关系切向上的合力 Fτ决定 V 的大小法向上的合力 Fn决定 V 的方向若是匀速圆周运动,切向上合力为零 Fτ=0 法向上的合力不为零 Fn≠0若是非匀速圆周运动,切向上的合力不为零 Fτ≠0 法向上的合力不为零 Fn≠0例:下列说法正确的是( )A.速度大小变化的越快,向心加速度越大B.速度方向变化的越快,向心加速度越大C.物体做匀速圆周运动时,向心加速度一定指向圆心D.物体做非匀速圆周运动时,向心加速度可能不指向圆心 用心 爱心 专心1例:一直棒 OP,下端用铰链固接,上端用手控制,可使其绕竖直轴并偏离 θ 角在水平面内做圆周运动。现有一环套于 A 处,OA=L,如图所示。若 θ=450 ,环与杆间的 μ=0.5,欲使环不动,则转动的角速度 ω=?解题思路:1)找对象--找准研究的物体2)找半径--找准物体的旋转面和旋转中心3)找向心力--分析受力情况,建立正交系定出向心力4)找关系式--法向上列出向心力关系方程,切向上及其它方向上列出相应的关联方程。5)找答案---解方程组,并适当讨论用心 爱心 专心2OPAθ(一)水平面内的圆周运动例:车辆转弯----汽车、火车、自行车练:1、求绳长为 L、倾角为 θ 的圆锥摆的摆动周期。2、四个物块 A、B、C、D 质量分别为 m、2m、2m、m,距盘心分别为L、L、2L、3L,它们与盘的 μ 均一样,如图所示。在转动的角速度 ω 从零逐渐增大的过程中,哪个物块先发生滑动?总结:1、2、用心 爱心 专心3θLABCDωA2R2LBRLm2m3、(二)竖直面内的圆周运动1、内轨(轻绳)模型2、外轨模型3、双轨(轻杆)模型练习1、图 1:小球在竖直面内做半个圆周运动;图 2:小球在竖直面内做完整的圆周运动;图 3:小球在斜面内做完整的圆周运动;三种情况下,绳子上下拉力之差为多少?用心 爱心 专心4·用心 爱心 专心5θ··